info@gerb.com
고층 빌딩의 시공사례를 통한 제진기술 연구자료 사용자의 안전과 편의성
세계초고층도시건축학회 (CTBUH – Council on Tall Buildings and Urban Habitat)의 제진시스템 가이드라인
Thyssen Krupp Test Tower, 독일 로트바일
프로젝트 상세정보
- 준공 연도:
2016년 (증축) - 시행사/시공사/발주사:
Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators - 건축 설계:
Werner Sobek Stuttgart 및 JAHN Architects Chicago 공동 설계 - 구조 설계:
Werner Sobek Stuttgart - 제진시스템 공급:
GERB Vibration Control Systems - 측정 및 점검:
Wacker Ingenieure (풍동 실험 및 엔지니어링) - 높이 / 층간 높이:
246m / 3.3m (오피스 구역) - 세장비 (Slenderness Ratio):
1/11.8 - 층수:
27개층 / 오피스 구역 8개층 - 건축물 총 면적:
340㎡ - 건축물 용도:
엘리베이터 성능검사 타워 / 사무실 / 관측대 (232m) - 건축 자재:
철근 콘크리트 (C50/60) / 강철 구조물에 PTFE 멤브레인 외벽 설치 - 구조 시스템:
매트 기초에 캔틸레버 (외팔보) 철근콘크리트 지지대 설치
(- 32m) - 적용된 제진기술:
하이브리드 질량 댐퍼 시스템 (240톤)

1.0 소개글 / 연혁
독일 남서부에 높이 246m의 엘레베이터 기술개발을 위한 고층의 대형 테스트 타워는 원형의 직경 20m 면적에 준공되었으며, 내부에 엘레베이터 통로 9개, 방재승강기 1대, 통유리 파노라마 뷰 엘레베이터 공간과 함께 엘레베이터 성능검사를 위한 220m의 기계 리프팅 통로가 마련되어 있습니다.
직경 40m의 빌딩 기초부에는 별도의 서비스 시설 및 로비, 교육 센터 공간이 있습니다. 232m 높이에 위치한 관측대는 독일에서 가장 높은 관측대로 슈바르츠발트의 멋진 경관을 확인할 수 있으며, 맑은 날씨에는 알프스 산맥까지 볼 수 있습니다.

2.0 구조 시스템:
테스트타워 빌딩의 구조시스템은 직경 20.8m의 철근 콘크리트 튜브를 기본으로 구성되어 있으며 지하 30m 깊이로 건물 둘레의 지반에 고정됩니다 (그림 2 참조). 해당 튜브는 높이 110m 까지는 두께가 40cm이고 그 위로는 25cm입니다. 기반이 상부 육성층과 하부 해성층으로 구성된 경우, 지지력이 높아 별도의 파일 기초가 필요하지 않습니다. 건축물이 넓은 지반에 고정되어 있는 동시에, 기초구조물의 규모가 넓어 수평강성이 더욱 높아졌습니다.
콘크리트 튜브의 내구성은 주로 승강기 통로의 내벽에 의해 결정됩니다. 엘리베이터에 접근할 수 있도록 특정 층에만 조립식 천장슬래브가 설치되어 있습니다. 일부 엘리베이터는 115m 높이로 현장에서 주조된 40cm 두께의 대경간으로 덮여 있습니다. 해당 층은 오피스 공간으로 사용되고 있습니다. 위로 197m 정도의 빈 공간에 열 저장체와 TMD 제진시스템가 설치되었습니다. 타워의 정상은 사무실 및 기타 엘리베이터를 위한 공간으로 사용되었습니다.

이 테스트 타워만의 독특한 특징은 PTFE 코팅의 유리섬유메시로 직물 외벽을 구성했다는 점입니다. 건물이 높아질수록 섬유메시를 더 넓은 폭으로 설치하여, 외벽의 투명도를 높이는 동시에 소재의 밀도와 중량을 낮추고 풍하중에 대한 저항도를 향상시켰습니다.
나선형의 외벽 디자인은 ‘Scructon Spiral’ 로 불리는 형태로, 풍하중 방지하는 동시에, 섬유망으로 콘크리트 구조물에 그늘을 만들어 태양 복사열까지 감소시키는 기능을 가지고 있습니다. 이 경우 외벽 설계와 건축재를 선택할 때에 시공과 유지관리, 내구성 외에 풍하중까지 함께 고려되어야 했습니다.
3.0 건축 공법

테스트 타워의 시공절차:
- 30m 원형수직구 지반 굴착 발파공법으로 굴착 및 모델링을 실시했습니다. 굴착 후 지반앵커와 콘크리트 보강벽체로 기초를 완성했습니다.
- 매트기초 타설
- 슬립 폼 공법으로 수직구 시공 4개월간 수직구 벽체 완공
- 기초슬래브 시공
- 출입구역 시공
4.0 풍하중에 대한 동적응답 예측
테스트 타워의 기본 주파수는 건축 단계와 콘크리트 상태(균열/비균열)에 따라 0.17Hz – 0.20Hz의 범위 내에 있을 것으로 예측되었습니다 – 그림 4 참조.
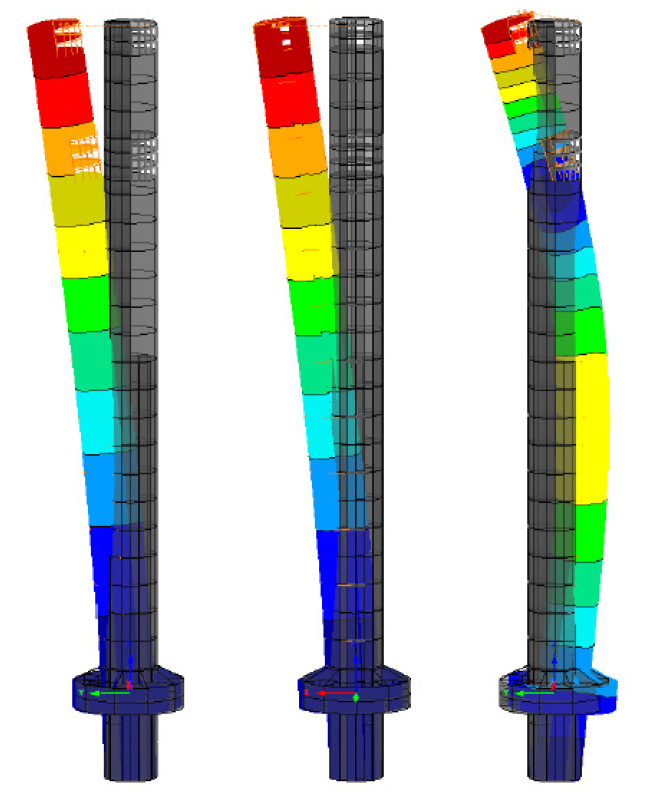
풍동 해석을 통해 55 – 60km/h 범위 내의 풍속에서 높이 10m에 해당하는 구조물 공진이 발생할 수 있다고 예측되었습니다. 추가적인 제진장치 없이는 진동이 약 +/- 750mm의 상층부 처짐을 유발하여, 건물 이용자들에게 불안감을 줄 뿐만 아니라, 전체 건축물 자체 수명에 상당한 영향을 줄 수 있다는 결론이 나왔습니다. (그림 5 참조). 횡방향 풍진동에 대한 동적응답을 줄이기 위해 수동형 TMD 제진시스템이 도입되었습니다. 타워가 건물의 흔들림에 민감한 승강기 설비에 대한 테스트 타워로 사용될 것이기 때문에, 발주자는
바람이 없는 날 인위적으로 타워를 흔들어, 그럼에도 불구하고 어떠한 피로 문제가 발생하지 않는 변위를 발생시킬 수 있는 방법을 찾았습니다. 인위적인 흔들림에 필요한 수준은 약 +/- 200mm라고 간주한 안전 범위 이내였습니다. 이러한 요청으로 인해 하이브리드 질량 댐퍼(Hybrid Mass Damper: HMD), 또는 이렇게 설계한 시스템이 과거에 도입된 다른 HMD 시스템에서 파생되었기 때문에 Dual Use TMD라고 칭하는 시스템을 구현할 수 있는 드문 기회가 주어졌습니다. 이 시스템은 다음 장에서 소개할 계정이며, 여기에는 피동형 시스템의 최적화, 액추에이터의 기계 장치 설계, 제어 알고리즘 및 안전 컨셉이 포함되어 있습니다.

5.0 피동형 TMD 제진 시스템의 최적화
피동형 TMD 시스템의 매개변수는 다음과 같은 세 가지 측면을 고려하여 결정되어야 합니다: a) 와류 발산 진동으로 인한 동적 응답을 감소시키기 위한 추가적인 구조적 댐핑력을 충분히 제공, b) 돌풍 발생 시 횡방향 풍진동에 대해, 피동 모드에서 충분한 댐핑력으로 TMD 메인 질량 이동을 달성할 수 있는/실제 값으로 제한, c) 공급한 액추에이터에 의해 이용할 수 있는 성능 범위를 고려하여, 타워의 원하는 최대 편향에 필요한 에너지 유입에 따라 여기 모드에서 TMD 질량 선택
(예: 발생한 최대 힘 및 작동 중 최대 스트로크). TMD 시스템을 최적화하기 위해 확인된 구조적 속성에서 보고된 것과 동일한 질량 관성 모멘트와 타워의 질량 분배를 나타내는 수치 모델을 사용하였습니다. 실물 크기의 관찰에서 나온 모드 형상과 고유 진동수를 일치시키기 위해 바닥판 사이의 강성 부재를 맞춤형으로 제조하였습니다. 그림 6 좌측에는 사용한 해당 아날로그 모델의 모드 형상과 고유 진동수가 표시되어 있습니다. 또한 그림 6 좌측에는 아날로그 모델의 모드 형상을 구조 컨설턴트가 준비한 상세한 모델의 모드 형상과 비교되어 있습니다.
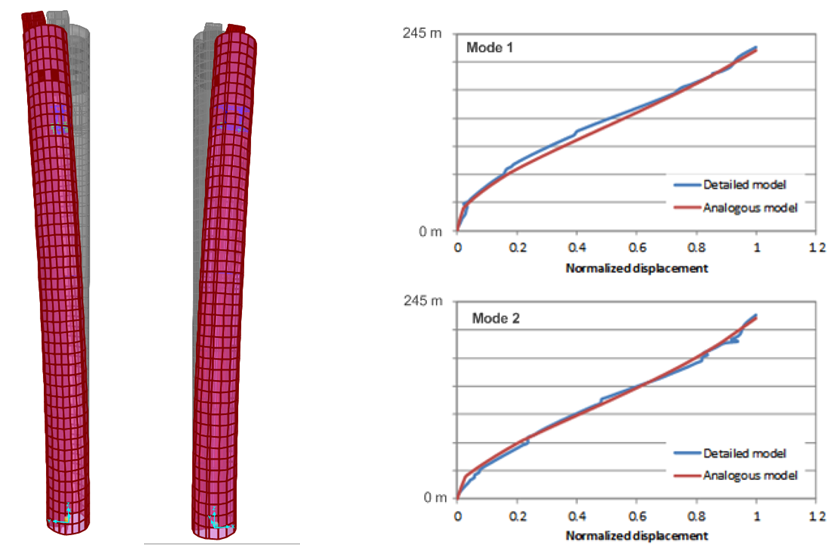
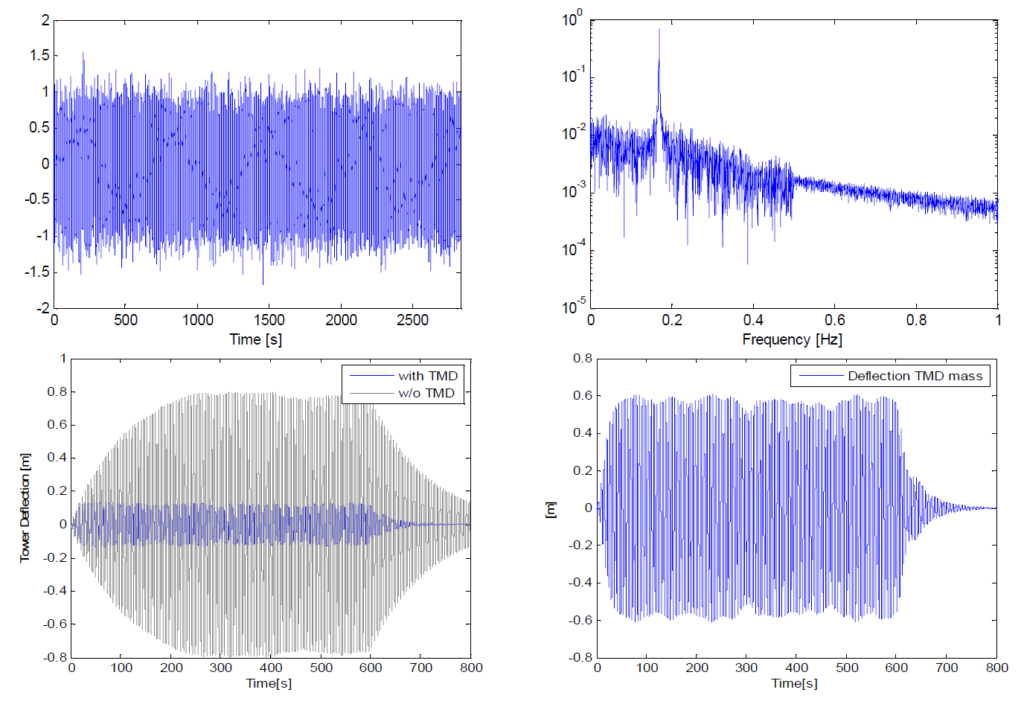
또한 TMD는 타워에서 자신의 편향된 위치를 수집하며, 진자형 시스템으로 별도로 모델화되었습니다. 통제적 입력 케이스를 위한 하중 특성은, 예를 들어 와류 발산으로 인한 공진 여기는 단일 조화 여기의 특성과 상당히 유사합니다. 그럼에도 불구하고 공존하는 돌풍 하중은 그 특성이 본질적으로 확률적이라는 점이며, 이를 위해 잘 알려진 Den Hartog 기준과 다른 최적화 기준이 적용됩니다. 또한 TMD 질량의 상대적 변위는 조화 유형의 하중보다 확률적 유형에서 더 큽니다. 최적의 TMD 매개변수를 수치로 결정하기 위해서는 실제에 가까운 하중을 고려해야 하기 때문에, (다벤포트 스펙트럼 기반) 확률적 돌풍 하중과 겹친 공진을 와류 발산과 유사한, 즉, 전반적인 횡방향 풍진동을 나타내기 위한 요소를 포함한 시간 이력을 생성하였습니다(그림 3 우측 참조). 최적화된 피동형 TMD 시스템으로 달성할 수 있는 타워의 편향 감소와 그로 인한 TMD 변위는 그림 3 우측에 표시되어 있습니다.
ξ=0.8%로 산정한 고유의 구조적 댐핑에 대한 이러한 결과를 기초로 하여, 최고의 TMD 성능을 위해 최적의 TMD 감쇠율을 유지하면서 +/- 650mm의 변위를 유지하려면 240톤의 TMD 질량이 필요했다고 판단했습니다. TMD 댐핑의 증가는 이동 거리를 감소시킬 수 있었습니다. 그 효율성은 여전히 충분하지만 이는 역으로 액추에이터의 힘에 대한 요구 사항에 영향을 주었습니다. 240톤 TMS를 최적으로 설치하기 위해 필요한 힘을 결정하기 위해, 아날로그 모델도 사용하여 타워의 변위가 +/- 200mm의 범위 내에서 이루어질 수 있다는 점을 검증하였으며, 이때 액추에이터에서 나온 최대 40kN의 힘을 사용하였습니다. 그림 4에는 아날로그 수치 모델을 사용한 시간 영역 수치 시뮬레이션 결과가 표시되어 있습니다; 이를 위해 결과적으로 발생한 타워 상부의 편향, TMD 질량 편향 및 이를 유발하는 유입된 능동적인 힘이 표시되어 있습니다.


6.0 제어 시스템에 대한 설명
제어 시스템의 이중성은 다음의 목적을 달성합니다: a) 정상적인 피동형 작동 중 진동 발생을 줄이기 위한 에너지 소비 감소 b) 실제로 요구되는 힘을 궁극적으로 달성하기 위해, 메인 TMD 질량 자극을 위한 공진 효과를 사용함으로써 액추에이터에 요구하는 힘의 감소 따라서 다른 제어 시스템(그림 1 참조)과 비교하자면, 액추에이터는 메인 구조물과 TMD 질량을 결합하지만 TMD 질량을 직접 제어하기 위해서는 사용되지 않습니다. 이러한 제어는 전형적인 능동형 질량 드라이버/댐퍼 시스템이 담당하기 때문입니다.
구현된 Dual Use TMD를 위해 240톤의 피동형 작동을 위한 반응 질량이 선택되었습니다. 여자 작동 모드의 경우 두 개의 선형 드라이브(각 주요 방향에 하나씩)의 인위적인 비틀림을 방지하기 위해 무게 중심 근처에 피벗이 있는 TMD 질량에 부착됩니다. 각 선형 드라이브는 최대 +/- 600mm의 스트로크 내에서 최고 40kN의 힘을 공급할 수 있습니다(세부 사항에 대해서는 그림 2 참조). 선형 드라이브는 탈거할 수 있으므로, 발생 가능성이 극히 낮으나 베어링 고장 시에도 액추에이터의 베어링에 의해 피동 모드 전체가 영향을 받지는 않습니다.
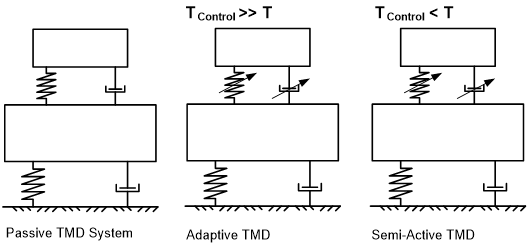
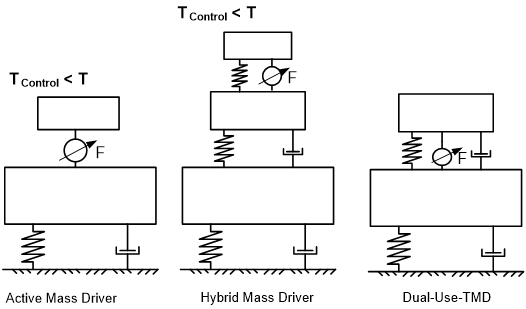
그림 10 – 제어 시스템 유형 – 피동형, 반능동형, 능동형 및 하이브리드 시스템과 비교한 Dual Use TMD
이 시스템에는 타워 상부의 높이 및 TMD 질량 가속도를 측정하기 위해 네 개의 단축 가속도계(지진 K-빔/MEMS; 각 방향에 하나씩)가 장착되어 있습니다. 가속 신호는 타워가 가지고 있는 기본적인 고유 주파수(0.1 – 0.3Hz)의 주파수 범위 내에서 대역 필터링되고, 타워의 가속도와 편향에 통합됩니다.
또한 신호 드리프트를 비교하기 위해 상부에도 설치한 무료 세계 항행 위성 시스템(Global Navigation Satellite System) 중 하나와 통합된 변위 값을 비교할 수 있습니다. 최초의 관련 테스트를 적절하게 수행했습니다. 더 나아가 스트링 포트 변환기를 사용하여 TMD 변위를 직접 모니터링하였으며 유도형 길이 측정 시스템을 선형 모터 내에 내장하였습니다.
7.0 제어 알고리즘
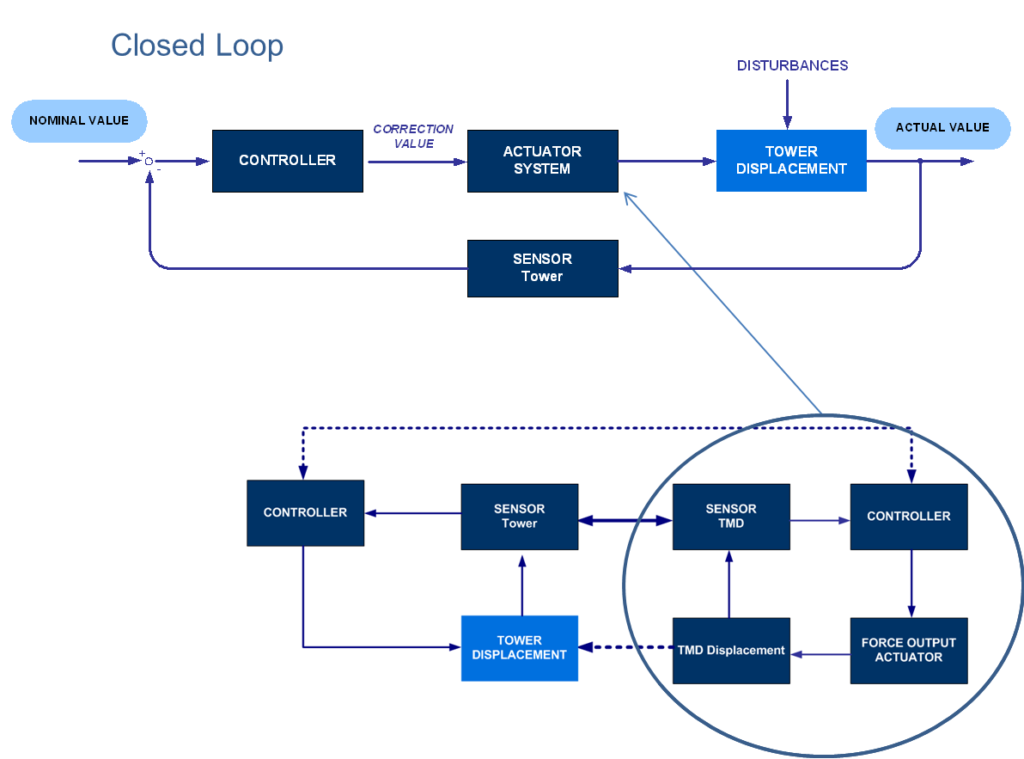
타워에 대한 일반적인 제어 루프는 폐쇄루프 제어 시퀀스를 설명한 그림 5에 표시되어 있습니다. 제어 알고리즘을 세부적으로 설계하기 위해서는 액추에이터-TMS 질량 사이의 상호 작용에 대한 분석적 모델이 필요합니다. 이는 적용된 작용력에 대해 액추에이터 입력부 사이의 연결을 결정하기 위해서입니다. 이것은 전체 건물의 동적 거동을 설명하는 주요 구조 해석 모델과 결합되어야 합니다. 더 나아가, 다음과 같이 다른 HMD 애플리케이션에 적용되었던 표준 제어 알고리즘과 비교 [2],[3] 또는 다음과 같이 이론적으로 조사 [1] 이 타워 애플리케이션에 대한 제어 알고리즘은 하나의 메인 방향에서의 제어된 여기와 직각 방향에서의 진동 감소를 동시에 고려해야 했습니다. 기본 모드에서는 대부분 동적 응답을 예상하므로, 불안전성을 방지하는 데 장점이 있는 선형 피드백 제어를 이 두 작업에 적용할 수 있었습니다. 단순한 제어를 실제로 구현하기 위해, 타워의 여기에 대한 수직 동적 반응을 약화시시키는 선형 피드백 제어는 7가지 동적 측정에 대한 명시적으로 가중된 선형 합계를 통해 관련 액추에이터를 작동시킵니다. 이 측정은 다음과 같습니다: TMD 및 타워 상부의 가속도, TMD 및 타워 상부의 속도, TMD 및 타워 상부의 변위, 그리고 타워 상부의 상대적 변위에 대한 TMD.
중요한 점은 사전에 선택한 가중 계수가 단순하며 양이나 음의 스칼라 게인라는 것입니다. 가중 계수의 매개변수 설정은 타워의 동적 테스트를 기반으로 하며 진동수에 종속된 어떠한 변경도 사용하지 않습니다. 능동적인 액추에이터 피드백을 즉시 (50Hz에서) 계산하며, 이는 다시 기존의 동적 측정의 선형 결합이 됩니다. 사용되는 비선형 조작은 없습니다. 제어 설계 역시 액추에이터 제어에 의해 진동 감쇠가 이루어진다는 것을 증명하는 시간 영역 수치 시뮬레이션(예: 직접 통합)으로 이루어졌습니다. 여기 모드의 경우, 타워가 원하는 변위 값으로 여기되는 것을 나타내는 변위 오프셋과 함께 동일한 제어 접근 방식이 사용되었습니다. 이 오프셋은 각 방향의 감지된 기본 진동수를 기반으로 한 사인 함수입니다. 그러면 다른 방해 요소에 의한 상부 변위의 진동에 대응하기 위한 제어 출력이 오프셋 사인 함수에 따라 변조되고 제어값도 이에 따라 조정됩니다.
여기에 타워의 수직 동적 응답을 감소시키기 위한 선형 피드백 제어는 액추에이터에 대한 힘 명령이 프로그램의 7가지 동적 측정의 지정된 가중 선형 합계가 됩니다. 7가지 측정은 다음과 같습니다: TMD 및 상부의 가속도, TMD 및 타워의 속도, TMD 및 타워의 변위, 그리고 타워의 상대적 변위에 대한 TMD. 중요한 점은 가중 계수가 단순하며 양이나 음의 스칼라 값이라는 것입니다. 가중 계수의 매개변수 설정은 타워의 실험적 동적 테스트를 기반으로 합니다. 액추에이터 피드백은 작동 중이며 즉시 계산됩니다(50Hz)
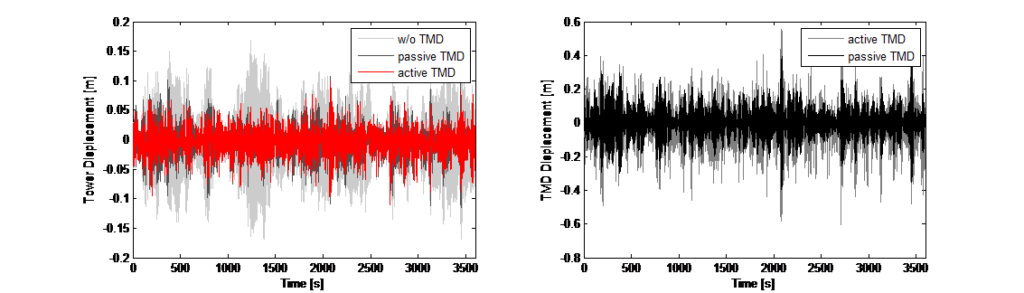
그리고 가중 계수는 스칼라 값이며, 이러한 계수는 어떠한 형태의 진동수 종속 전달 함수도 사용하지 않습니다. 따라서 이 피드백은 동적 속성의 선형 결합입니다. 사용되고 있는 비선형 조작 또는 로직은 없습니다. 제어 설계이 시간 영역에서의 수치 시뮬레이션(직접 통합)을 위해 이루어졌으므로, 각 시간 단계에 대해 액추에이터 제어로서 TMD 질량에 대한 강제 입력을 조절할 수 있었습니다. 그림 12는 진동 억제에 대한 시뮬레이션에서 나온 결과를 보여줍니다. 즉, 타워 변위 및 이로 인한 TMD 질량의 이동 거리입니다.
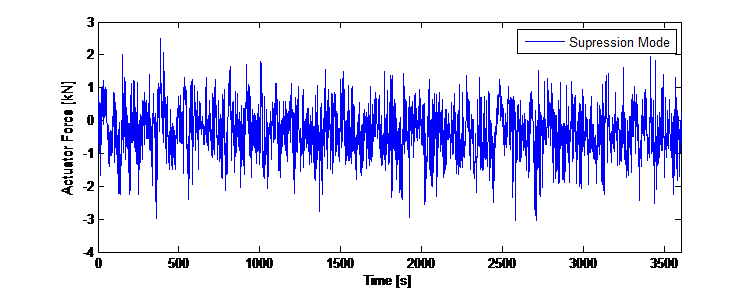
여기 모드의 경우, 타워가 원하는 변위 값으로 여기되는 것을 나타내는 오프셋과 함께 동일한 제어 접근 방식이 사용되었습니다. 이 오프셋은 각 방향에 대해 감지된 기본 진동수를 기반으로 한 사인 함수입니다. 그러면 방해 요소에 의한 상부 변위의 진동에 대응하기 위한 제어 출력이 오프셋 사인 함수에 따라
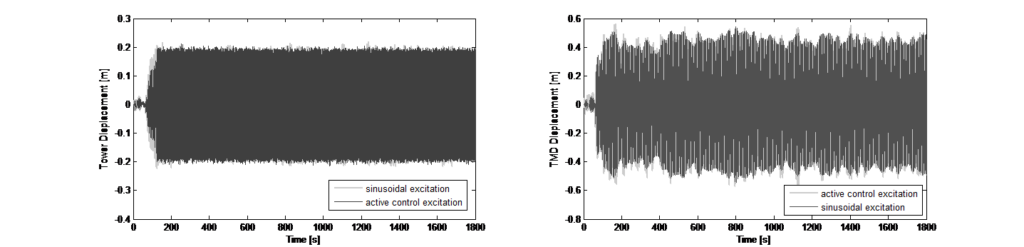
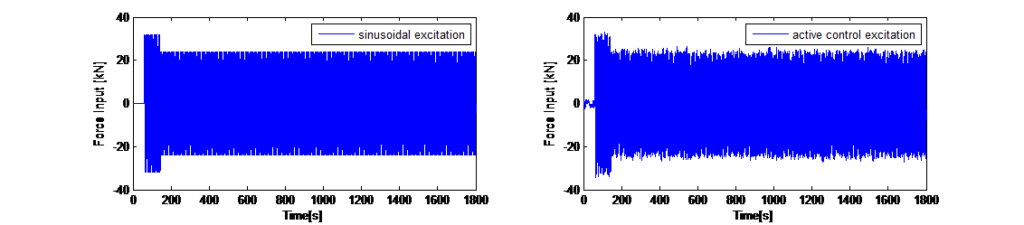
변조되고 제어값도 이에 따라 조정됩니다. 이 오프셋에 대해 가중 계수가 실험에 의해 결정되었습니다. 그림 13은 단순 사인 곡선 여기와 제어 알고리즘이 적용된 여기 모드에 대한 돌풍 하중 방해에 대한 결과를 수치적으로 제시합니다.
8.0 안전 컨셉
액추에이터로 사용된 선형 드라이브가 제공할 수 있는 +/- 40kN의 힘을 고려하면, 타워 변위가 피로 규정을 초과하지 않는 것을 보장하는 안전 개념이 필수적입니다. 이는 힘의 출력이 충분하지 않아 상부 편향이 사전에 규정된 +/-200mm보다 크지 않는 경우에도 적용됩니다. 시스템의 안전을 더욱 개선하는 한 가지 방법은 타워의 상단 편향을 기록하는 모니터링 센서 중복을 증가시키는 것입니다. 이를 달성하기 위한 가장 좋은 방법은 실제 제어 하드웨어와 다른 측정 원리를 이상적으로 사용하는 독립된 모니터링 시스템을 추가하는 것입니다. 여기서 소개한 프로젝트의 경우, 사용한 제어 하드웨어는 이미 언급한 것과 같이 가속도계와 구조물의 관련 고유 진동수 범위 내에서 신호 대역 필터링을 위한 정의된 가속 임계값을 사용하였습니다. 가장 중요한 상위 모니터링 시스템은 정확도가 +/- 10mm인 세계 항행 위성 시스템(Global Navigation Satellite System: GNSS)입니다.
이 GNNS 시스템에는 좌표 데이터를 실제 변위 응답값으로 처리하는 기준 베이스 스테이션이 필요합니다. 타워의 상부 변위가 인위적인, 즉 추가적인 바람이나 기타 다른 여기에 의한 것일 수 있는 여기 모드 중 사전에 지정된 임계값을 초과하면, 릴레이가 출석 신호를 0V로 전환합니다. 그러면 여기 모드가 중단될 것입니다. 또한 두 모니터링 시스템은 수집한 데이터에 결함이 있는 센서 신호가 있는지 여부를 지속적으로 점검하여, 활성 여기 모드가 중단됩니다. 잘못된 가속/스트링 포트 신호는 스펙트럼 극대값 검출 기준에 의해 감지됩니다. 관련 범위 내에서의 극대값 검출이 가능한 경우에만 센서가 올바른 신호를 제공한다고 가정할 수 있습니다. GNNS 시스템이 좌표 데이터의 변경을 분석할 때, 샘플링한 데이터가 적시에 변경되지 않으면, 그 신호는 자동으로 틀린 신호로 간주됩니다.
9.0 진동 테스트
타워에 대한 최초의 진동 테스트는 그 타워가 아직 준공되지 않은 단계에서 수행되었기 때문에, 이 단계에서 타워의 기본 진동수는 피동형 TMD 시스템의 명시된 동조 범위 이상입니다. TMD를 가능한 한 가장 높은 동조 진동수로 조절하였습니다. 이 진동 테스트의 목표는 차단된 TMD 시스템과 고유한 구조적 댐핑력을 사용하여 타워의 기본 진동수를 측정하는 것이었습니다. 또한 피동형 TMS 시스템을 연결했을 때의 진동 거동과 피동형 TMD 시스템으로 인한 구조적 댐핑력의 증가도 측정할 것입니다. 타워의 기본 고유 진동수를 확인하기 위해 평균 정규화 파워 스펙트럼 밀도(Averaged Normalized Power Spectral Density: ANPSD) 방식을 [1] 사용할 수 있습니다. 이를 위해 기록한 시간 이력을 여러 세그먼트로 분리했습니다. 이러한 세그먼트를 진동수 영역으로 변환시켜야 합니다. 결과로 얻은 스펙트럼을 정규화 및 평균화하여 복소 공액 스펙트럼으로 곱해야 합니다.
이렇게 하면, 일정하기 않은 진동이 모두 제거되고 반복적으로 발생하는 구조물의 자유 진동만이 평균 스펙트럼에 표시되며, 이것은 이제 타워의 여기된 우세 고유 진동수를 나타냅니다. 그림 14는 차단된 TMD 사용 시, x 및 y 방향에서의 수평 주변 진동에 대해 기록한 시간 이력을 나타냅니다 그림 14 우측에는 120초의 세그먼트 길이에 대한 평균 오토 파워 스펙트라(Auto Power Spectra)가 표시되어 있습니다. 이 스펙트럼은 타워가 두 진동수(x 방향에서 0.225Hz 및 y 방향에서 0.245Hz)에서 동적 응답을 보인다는 것을 확인할 수 있도록 합니다.
주변 여기가 관련 진동 모드에서 충분한 동적 응답을 유발하여 확률적으로 안정성을 얻는다고 가정하는 위에서 설명한 평균 전력 스펙트럼 방법에 추가적으로, 고유 주파수는 상용 신호 처리 소프트웨어인 ARTEMIS를 사용하여 결정되었습니다. [1] 이 소프트웨어는 개선된 주파수 영역 분해(Enhanced Frequency Domain Decomposition) 및 확률적 부분공간 식별(Stochastic Subspace Identification) 방법을 통합합니다.
개선된 주파수 영역 분해(Enhanced Frequency Domain Decomposition: EFDD)와 확률적 부분공간 식별(Stochastic Subspace Identification)은 출력 전용 모달 매개변수 식별에 널리 사용되는 기법입니다.
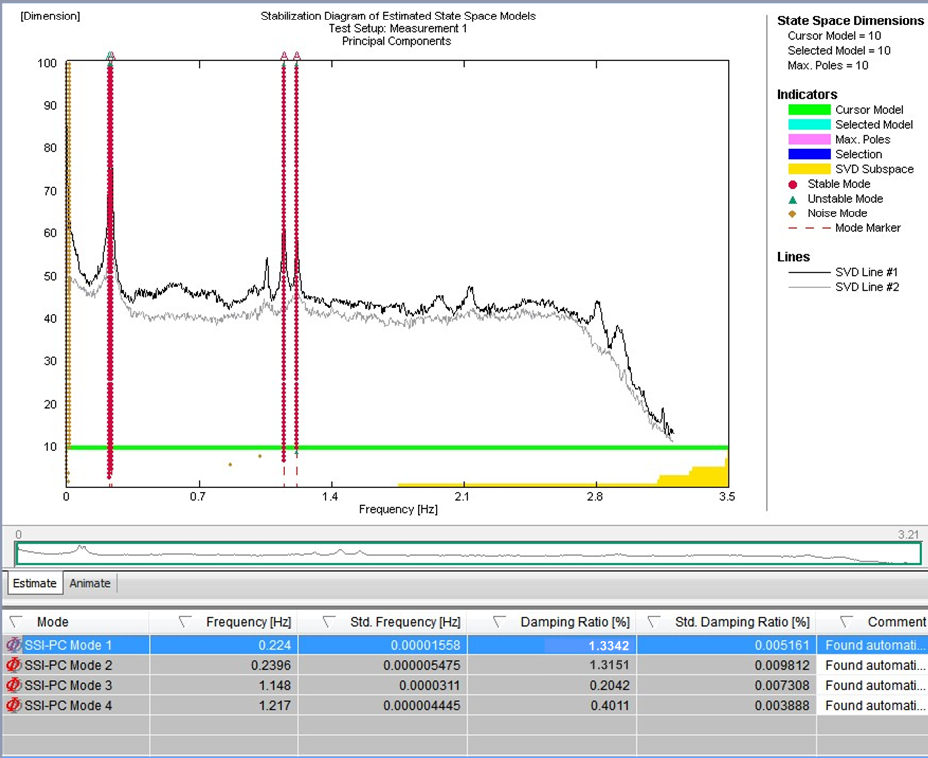
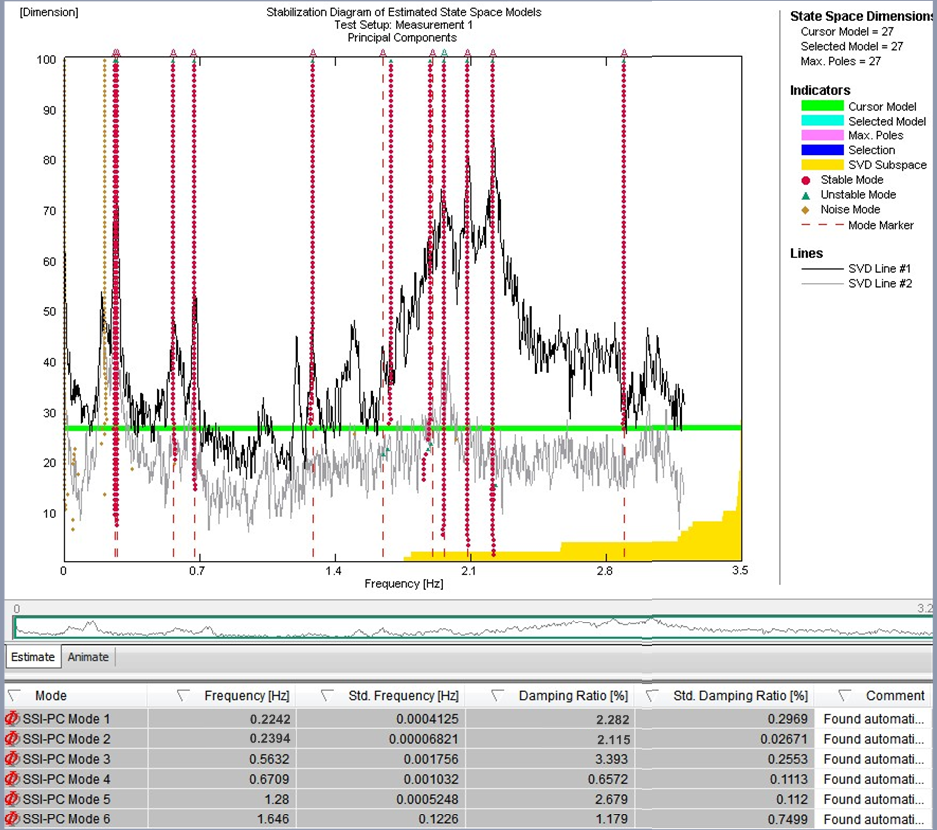
그림 15 – 차단된 TMD(좌측)과 활성화된 TMD(우측)을 사용하여 주변 진동을 기록하기 위한 안정성 카드(Stability Card)
EFDD 방식은 응답 스펙트럼의 계산을 기반으로 합니다. 그러므로 스펙트럼 평가에서 오류를 낮추고 모달 매개변수를 신뢰할 수 있는 방법으로 추출하기 위해서는 장기간의 기록이 필요합니다. 출력 전용 모델을 사용하여 교량을 확인하기 위해 확률적 부분공간 식별 알고리즘을 적용하였습니다. 확률적 부분공간 식별 방식은 시간 영역에서 사용되며 동적 문제의 상태 공간 설명을 기반으로 합니다. 서로 다른 모델 차수의 시스템 식별 결과를 비교하여, 소위 안정화 도표라고 하는 것에서 실제 구조 모드를 스퓨리어스 모드와 구별하였습니다. 이 도표는 확인된 시스템 모델을 선택할 때 일반적으로 사용되는 방법입니다. 실제 구조 모드는 자동화된 절차에서 평가된 특정 안정화 기준을 충족시키며 연속적인 모델 순서에 대해 안정적인 경향을 보이기 때문입니다. 그림 15는 관련 모드를 결정할 수 있도록 기록된 주변 데이터에 대한 결과 안정성 카드를 보여줍니다. 확인된 모드와 차단된 TMD(좌측) 및 연결된 TMD(우측)를 사용한 상태에서 측정한 감쇠율은 그림 14에도 표시되어 있습니다. 구조적 감쇠 증가를 확인할 수 있습니다. 추가적인 구조적 감쇠는 비동조 TMD 설정을 고려한 이론적 모델에서 결정할 수 있는 이론적 값 범위 내에 있습니다.
피동형 TMD 시스템을 사용한 주변 진동 테스트 외에도, TMD 시스템이 비동조 상태에 있음에도 불구하고 능동적인 여기 모드를 이용한 예비 테스트를 수행하였습니다. 그림 12 좌측은 타워의 상부에서 기록한 가속도에 대한 시간 이력을 나타냅니다. 최초의 사인파 여기 후, 타워 편향과 TMD 질량의 강제 변위 사이의 상관 관계를 실험적으로 측정하기 위해 정상 상태의 가속도 레벨을 위한 알고리즘을 이용할 수 있었습니다. 그림 12에 표시된 시간 이력은 여기 모드에서의 두 가지 테스트 시나리오를 나타내고 이에 상응하는 FFT 스펙트럼은 타워가 두 기본 주파수(x 및 y 방향)로 보내는 명확한 응답을 표시합니다. 녹색으로 표시된 시간 영역은 두 기본 방향에서 동적 응답을 야기한, 능동형 제어가 비활성화된 질량의 사인파 여기입니다. 이로 인한 FFT 스펙트럼은 이 두 방향의 기본 진동수를 식별하기 위한 두 극대값을 나타냅니다. 청색으로 표시된 세그먼트는 활성화된 능동형 제어가 있는 여기를 위한 것으로, 이는 한 방향에서 우세한 더 안정적인 타워 변위를 유발합니다. 여기 모드가 꺼진 후 발생하는 진동 약화는 구조적 댐핑을 측정하기 위해 사용되었으며, D=2.4%로 결정되었습니다. 이 결과는 SSI 알고리즘으로 결정한 감쇠율과 상관 관계가 있습니다.
10.0 결론 및 전망
Dual Use TMD를 246m 높이의 Thyssen Krupp Test-Tower에 설치했으며, 그 목표는 이 타워를 자체적인 기본 진동수로에서 제어된 동적 응답으로 의도적으로 여기시키는 것이었습니다. 이러한 여기의 목표는 타워의 두 기본 방향에서 건물을 정의된 바와 같이 흔드는 것입니다. 수치 계산을 기반으로 하여, 피동 모드에서 필요한 추가적인 감쇠를 달성하고 +/- 200mm의 타워 상부 변위를 달성하기 위해 필요한 제어력을 생성하기 위해서는 240톤의 TMD 질량이 필요하다는 것이 밝혀졌습니다. 여기 모드에 대해 정상 상태의 변위 레벨를 생성하고 직각 방향에서 바람과 강제 진동 요소에 의해 야기된 변위를 억제하기 위해 제어 알고리즘을 개발하고 수치 시뮬레이션으로 이를 테스트하였습니다. 사전에 제작된 콘크리트 슬래브를 사용한 진자 유형의 피동형 TMD 시스템을 설치한 후 액추에이터를 시운전하여 최초의 테스트를 수행하였습니다. 이 테스트로 타워의 고유 감쇠력이 예상했던 것보다는 높다는 것을 확인했으나 관련된 모든 모드를 명확히 결정할 수 있었습니다. 건물의 능동형 여기 모드가 작동하고 있으며, 건물이 아직 완전히 완성되지 않았기 때문에 모든 작동 매개변수를 도출할 수 있는 전체 범위는 아니지만 테스트를 실행할 수 있었습니다. 건물이 아직 완성 단계에 있지 않았기 때문에 TMD를 측정된 기본 진동수에 맞추어 조절할 수 없었습니다.
TMD 시스템을 조절하는 즉시, 진폭에 따른 댐핑 및 안전 개념의 무결성에 관한 테스트를 포함하여, 빌딩에 대한 후속 테스트가 수행됩니다.
참고 자료
[1] Wenzel, H., Pichler, D., Schedler, R. (1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.: Mevel, L. (2012). “Operational Modal Analysis using a Fast Stochastic Subspace Identification Method”, Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T., Spencer, J.R. (2000). “Active, Semi-Active and hybrid control of structures” In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Passive and active mass damper control of the response of tall buildings to wind gustiness. Eng. Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24–29.
[8] Soong, T.T. “Active Structural Control: Theory and Practice”; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008).”Active Control of Structures”, Wiley, Padstow
기타 자원
이 주제에 대한 더 자세한 정보가 필요하십니까?
문제가 있으시면 언제든 당사에 연락하시기 바랍니다.
당사의 프로젝트 엔지니어가 곧 답을 드릴 것입니다.
고층 빌딩의 시공사례를 통한 제진기술 연구자료 사용자의 안전과 편의성
세계초고층도시건축연합(Council on Tall Buildings and Urban Habitat: CTBUH)의 댐핑 시스템 가이드라인
Thyssen Krupp Test Tower, 독일 로트바일
프로젝트 상세정보
- 준공 연도:
2016년 (증축) - 시행사/시공사/발주사:
Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators - 건축 설계:
Werner Sobek Stuttgart 및 JAHN Architects Chicago 공동 설계 - 구조 설계:
Werner Sobek Stuttgart - 제진시스템 공급:
GERB Vibration Control Systems - 측정 및 점검:
Wacker Ingenieure (풍동 실험 및 엔지니어링) - 높이 / 층간 높이:
246m / 3.3m (오피스 구역) - 층수:
27개층 / 오피스 구역 8개층 - 건축물 총 면적:
340㎡ - 건축물 용도:
엘리베이터 성능검사 타워 / 사무실 / 관측대 (232m) - 적용된 제진기술:
하이브리드 질량 댐퍼 시스템 (240톤)

- 건축 자재:
철근 콘크리트 (C50/60) / 강철 구조물에 PTFE 멤브레인 외벽 설치 - 구조 시스템:
매트 기초에 캔틸레버 (외팔보) 철근콘크리트 지지대 설치
(- 32m)
고층 빌딩의 시공사례를 통한 제진기술 연구자료 사용자의 안전과 편의성
세계초고층도시건축연합(Council on Tall Buildings and Urban Habitat: CTBUH)의 댐핑 시스템 가이드라인
Thyssen Krupp Test Tower, Rottweil/Germany
프로젝트 상세정보
- 준공 연도: 2016년(목표 높이 달성)
- 시행사/시공자/발주사: Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators
- 건축 설계사: Werner Sobek, JAHN Architects Stuttgart 및 Chicago와 공동 작업
- 구조 설계사: Werner Sobek Stuttgart
- 댐핑 시스템 공급사: GERB Vibration Control Systems
- 시험 실험실: Wacker Ingenieure(풍력 공학 / 풍동 테스트)
- 높이 / 층간 높이: 246m / 3.3m(사무실 공간)
- 층수: 27개의 높이 / 8개 층의 사무실 공간
- 타워의 총 면적: 340제곱미터
- 건물의 기능: 엘리베이터 시험 타워 / 사무실 / 관찰 플랫폼(232m)
- 건축재: 철근 콘크리트(C50/60) / 강철 구조물에 설치한 PTFE 멤브레인 외벽
- 구조 시스템: 래프트 기초 위의 칸틸레버 철근 콘크리트 코어(- 32 m)
- 사용한 댐핑 전략: 하이브리드 질량 댐퍼 시스템(240톤)

1.0 소개글 / 연혁
독일 남서부에 높이 246m의 엘레베이터 기술개발을 위한 고층의 대형 테스트 타워는 원형의 직경 20m 면적에 준공되었으며, 내부에 엘레베이터 통로 9개, 방재승강기 1대, 통유리 파노라마 뷰 엘레베이터 공간과 함께 엘레베이터 성능검사를 위한 220m의 기계 리프팅 통로가 마련되어 있습니다.
직경 40m의 빌딩 기초부에는 별도의 서비스 시설 및 로비, 교육 센터 공간이 있습니다. 232m 높이에 위치한 관측대는 독일에서 가장 높은 관측대로 슈바르츠발트의 멋진 경관을 확인할 수 있으며, 맑은 날씨에는 알프스 산맥까지 볼 수 있습니다.

2.0 구조 시스템:
테스트타워 빌딩의 구조시스템은 직경 20.8m의 철근 콘크리트 튜브를 기본으로 구성되어 있으며 지하 30m 깊이로 건물 둘레의 지반에 고정됩니다 (그림 2 참조). 해당 튜브는 높이 110m 까지는 두께가 40cm이고 그 위로는 25cm입니다. 기반이 상부 육성층과 하부 해성층으로 구성된 경우, 지지력이 높아 별도의 파일 기초가 필요하지 않습니다. 건축물이 넓은 지반에 고정되어 있는 동시에, 기초구조물의 규모가 넓어 수평강성이 더욱 높아졌습니다.
콘크리트 튜브의 내구성은 주로 승강기 통로의 내벽에 의해 결정됩니다. 엘리베이터에 접근할 수 있도록 특정 층에만 조립식 천장슬래브가 설치되어 있습니다. 일부 엘리베이터는 115m 높이로 현장에서 주조된 40cm 두께의 대경간으로 덮여 있습니다. 해당 층은 오피스 공간으로 사용되고 있습니다. 위로 197m 정도의 빈 공간에 열 저장체와 TMD 제진시스템가 설치되었습니다. 타워의 정상은 사무실 및 기타 엘리베이터를 위한 공간으로 사용되었습니다.

이 테스트 타워만의 독특한 특징은 PTFE 코팅의 유리섬유메시로 직물 외벽을 구성했다는 점입니다. 건물이 높아질수록 섬유메시를 더 넓은 폭으로 설치하여, 외벽의 투명도를 높이는 동시에 소재의 밀도와 중량을 낮추고 풍하중에 대한 저항도를 향상시켰습니다.
나선형의 외벽 디자인은 ‘Scructon Spiral’ 로 불리는 형태로, 풍하중 방지하는 동시에, 섬유망으로 콘크리트 구조물에 그늘을 만들어 태양 복사열까지 감소시키는 기능을 가지고 있습니다. 이 경우 외벽 설계와 건축재를 선택할 때에 시공과 유지관리, 내구성 외에 풍하중까지 함께 고려되어야 했습니다.
3.0 건축 공법

테스트 타워의 시공절차:
- 30m 원형수직구 지반 굴착 발파공법으로 굴착 및 모델링을 실시했습니다. 굴착 후 지반앵커와 콘크리트 보강벽체로 기초를 완성했습니다.
- 매트기초 타설
- 슬립 폼 공법으로 수직구 시공 4개월간 수직구 벽체 완공
- 기초슬래브 시공
- 출입구역 시공
4.0 풍하중에 대한 동적응답 예측
테스트 타워의 기본 진동수는 건축 단계와 콘크리트의 상태(균열/비균열)에 따라 0.17Hz – 0.20Hz의 범위 내에 있을 것으로 예측하였습니다 – 그림 4 참조.

풍동 해석을 통해 55 – 60km/h 범위 내의 풍속에서 높이 10m에 해당하는 구조물 공진이 발생할 수 있다고 예측되었습니다. 추가적인 제진장치 없이는 진동이 약 +/- 750mm의 상층부 처짐을 유발하여, 건물 이용자들에게 불안감을 줄 뿐만 아니라, 전체 건축물 자체 수명에 상당한 영향을 줄 수 있다는 결론이 나왔습니다. (그림 5 참조). 횡방향 풍진동에 대한 동적응답을 줄이기 위해 수동형 TMD 제진시스템이 도입되었습니다. 타워가 건물의 흔들림에 민감한 승강기 설비에 대한 테스트 타워로 사용될 것이기 때문에, 발주자는 바람이 없는 날 인위적으로 타워를 흔들어, 그럼에도 불구하고 어떠한 피로 문제가 발생하지 않는 변위를 발생시킬 수 있는 방법을 찾았습니다. 인위적인 흔들림에 필요한 수준은 약 +/- 200mm라고 간주한 안전 범위 이내였습니다. 이러한 요청으로 인해 하이브리드 질량 댐퍼(Hybrid Mass Damper: HMD), 또는 이렇게 설계한 시스템이 과거에 도입된 다른 HMD 시스템에서 파생되었기 때문에 Dual Use TMD라고 칭하는 시스템을 구현할 수 있는 드문 기회가 주어졌습니다. 이 시스템은 다음 장에서 소개할 계정이며, 여기에는 피동형 시스템의 최적화, 액추에이터의 기계 장치 설계, 제어 알고리즘 및 안전 컨셉이 포함되어 있습니다.

5.0 피동형 TMD 제진 시스템의 최적화
피동형 TMD 시스템의 매개변수는 다음과 같은 세 가지 측면을 고려하여 결정되어야 합니다: a) 와류 발산 진동으로 인한 동적 응답을 감소시키기 위한 추가적인 구조적 댐핑력을 충분히 제공, b) 돌풍 발생 시 횡방향 풍진동에 대해, 피동 모드에서 충분한 댐핑력으로 TMD 메인 질량 이동을 달성할 수 있는/실제 값으로 제한, c) 공급한 액추에이터에 의해 이용할 수 있는 성능 범위를 고려하여, 타워의 원하는 최대 편향에 필요한 에너지 유입에 따라 여기 모드에서 TMD 질량 선택 (예: 발생한 최대 힘 및 작동 중 최대 스트로크). TMD 시스템을 최적화하기 위해 확인된 구조적 속성에서 보고된 것과 동일한 질량 관성 모멘트와 타워의 질량 분배를 나타내는 수치 모델을 사용하였습니다. 실물 크기의 관찰에서 나온 모드 형상과 고유 진동수를 일치시키기 위해 바닥판 사이의 강성 부재를 맞춤형으로 제조하였습니다. 그림 6 좌측에는 사용한 해당 아날로그 모델의 모드 형상과 고유 진동수가 표시되어 있습니다. 또한 그림 6 좌측에서는 아날로그 모델의 모드 형상을 구조 컨설턴트가 준비한 상세한 모델의 모드 형상과 비교하고 있습니다.


또한 TMD는 타워에서 자신의 편향된 위치를 수집하며, 진자형 시스템으로 별도로 모델화되었습니다. 통제적 입력 케이스를 위한 하중 특성은, 예를 들어 와류 발산으로 인한 공진 여기는 단일 조화 여기의 특성과 상당히 유사합니다. 그럼에도 불구하고 공존하는 돌풍 하중은 그 특성이 본질적으로 확률적이라는 점이며, 이를 위해 잘 알려진 Den Hartog 기준과 다른 최적화 기준이 적용됩니다. 또한 TMD 질량의 상대적 변위는 조화 유형의 하중보다 확률적 유형에서 더 큽니다. 최적의 TMD 매개변수를 수치로 결정하기 위해서는 실제에 가까운 하중을 고려해야 하기 때문에, (다벤포트 스펙트럼 기반) 확률적 돌풍 하중과 겹친 공진을 와류 발산과 유사한, 즉, 전반적인 횡방향 풍진동을 나타내기 위한 요소를 포함한 시간 이력을 생성하였습니다(그림 3 우측 참조). 최적화된 피동형 TMD 시스템으로 달성할 수 있는 타워의 편향 감소와 그로 인한 TMD 변위는 그림 3 우측에 표시되어 있습니다.
ξ=0.8%로 산정한 고유의 구조적 댐핑에 대한 이러한 결과를 기초로 하여, 최고의 TMD 성능을 위해 최적의 TMD 감쇠율을 유지하면서 +/- 650mm의 변위를 유지하려면 240톤의 TMD 질량이 필요했다고 판단했습니다. TMD 댐핑의 증가는 이동 거리를 감소시킬 수 있었습니다. 그 효율성은 여전히 충분하지만 이는 역으로 액추에이터의 힘에 대한 요구 사항에 영향을 주었습니다. 240톤 TMS를 최적으로 설치하기 위해 필요한 힘을 결정하기 위해, 아날로그 모델도 사용하여 타워의 변위가 +/- 200mm의 범위 내에서 이루어질 수 있다는 점을 검증하였으며, 이때 액추에이터에서 나온 최대 40kN의 힘을 사용하였습니다. 그림 4에는 아날로그 수치 모델을 사용한 시간 영역 수치 시뮬레이션 결과가 표시되어 있습니다; 이를 위해 결과적으로 발생한 타워 상부의 편향, TMD 질량 편향 및 이를 유발하는 유입된 능동적인 힘이 표시되어 있습니다.


6.0 제어 시스템에 대한 설명
제어 시스템의 이중성은 다음의 목적을 달성합니다: a) 정상적인 피동형 작동 중 진동 발생을 줄이기 위한 에너지 소비 감소 b) 실제로 요구되는 힘을 궁극적으로 달성하기 위해, 메인 TMD 질량 자극을 위한 공진 효과를 사용함으로써 액추에이터에 요구하는 힘의 감소 따라서 다른 제어 시스템(그림 1 참조)과 비교하자면, 액추에이터는 메인 구조물과 TMD 질량을 결합하지만 TMD 질량을 직접 제어하기 위해서는 사용되지 않습니다. 이러한 제어는 전형적인 능동형 질량 드라이버/댐퍼 시스템이 담당하기 때문입니다.
구현된 Dual Use TMD를 위해 240톤의 피동형 작동을 위한 반응 질량이 선택되었습니다. 여자 작동 모드의 경우 두 개의 선형 드라이브(각 주요 방향에 하나씩)의 인위적인 비틀림을 방지하기 위해 무게 중심 근처에 피벗이 있는 TMD 질량에 부착됩니다. 각 선형 드라이브는 최대 +/- 600mm의 스트로크 내에서 최고 40kN의 힘을 공급할 수 있습니다(세부 사항에 대해서는 그림 2 참조). 선형 드라이브는 탈거할 수 있으므로, 발생 가능성이 극히 낮으나 베어링 고장 시에도 액추에이터의 베어링에 의해 피동 모드 전체가 영향을 받지는 않습니다.


그림 10 – 제어 시스템 유형 – 피동형, 반능동형, 능동형 및 하이브리드 시스템과 비교한 Dual Use TMD
이 시스템에는 타워 상부의 높이 및 TMD 질량 가속도를 측정하기 위해 네 개의 단축 가속도계(지진 K-빔/MEMS; 각 방향에 하나씩)가 장착되어 있습니다. 가속 신호는 타워가 가지고 있는 기본적인 고유 주파수(0.1 – 0.3Hz)의 주파수 범위 내에서 대역 필터링되고, 타워의 가속도와 편향에 통합됩니다.
또한 신호 드리프트를 비교하기 위해 상부에도 설치한 무료 세계 항행 위성 시스템(Global Navigation Satellite System) 중 하나와 통합된 변위 값을 비교할 수 있습니다. 최초의 관련 테스트를 적절하게 수행했습니다. 더 나아가 스트링 포트 변환기를 사용하여 TMD 변위를 직접 모니터링하였으며 유도형 길이 측정 시스템을 선형 모터 내에 내장하였습니다.
7.0 제어 알고리즘
타워에 대한 일반적인 제어 루프는 폐쇄루프 제어 시퀀스를 설명한 그림 5에 표시되어 있습니다. 제어 알고리즘을 세부적으로 설계하기 위해서는 액추에이터-TMS 질량 사이의 상호 작용에 대한 분석적 모델이 필요합니다. 이는 적용된 작용력에 대해 액추에이터 입력부 사이의 연결을 결정하기 위해서입니다. 이것은 전체 건물의 동적 거동을 설명하는 주요 구조 해석 모델과 결합되어야 합니다. 더 나아가, 다음과 같이 다른 HMD 애플리케이션에 적용되었던 표준 제어 알고리즘과 비교 [2],[3] 또는 다음과 같이 이론적으로 조사 [1] 이 타워 애플리케이션에 대한 제어 알고리즘은 하나의 메인 방향에서의 제어된 여기와 직각 방향에서의 진동 감소를 동시에 고려해야 했습니다. 기본 모드에서는 대부분 동적 응답을 예상하므로, 불안전성을 방지하는 데 장점이 있는 선형 피드백 제어를 이 두 작업에 적용할 수 있었습니다. 단순한 제어를 실제로 구현하기 위해, 타워의 여기에 대한 수직 동적 반응을 약화시시키는 선형 피드백 제어는 7가지 동적 측정에 대한 명시적으로 가중된 선형 합계를 통해 관련 액추에이터를 작동시킵니다. 이 측정은 다음과 같습니다: TMD 및 타워 상부의 가속도, TMD 및 타워 상부의 속도, TMD 및 타워 상부의 변위, 그리고 타워 상부의 상대적 변위에 대한 TMD.
중요한 점은 사전에 선택한 가중 계수가 단순하며 양이나 음의 스칼라 게인라는 것입니다. 가중 계수의 매개변수 설정은 타워의 동적 테스트를 기반으로 하며 진동수에 종속된 어떠한 변경도 사용하지 않습니다. 능동적인 액추에이터 피드백을 즉시 (50Hz에서) 계산하며, 이는 다시 기존의 동적 측정의 선형 결합이 됩니다. 사용되는 비선형 조작은 없습니다. 제어 설계 역시 액추에이터 제어에 의해 진동 감쇠가 이루어진다는 것을 증명하는 시간 영역 수치 시뮬레이션(예: 직접 통합)으로 이루어졌습니다. 여기 모드의 경우, 타워가 원하는 변위 값으로 여기되는 것을 나타내는 변위 오프셋과 함께 동일한 제어 접근 방식이 사용되었습니다. 이 오프셋은 각 방향의 감지된 기본 진동수를 기반으로 한 사인 함수입니다. 그러면 다른 방해 요소에 의한 상부 변위의 진동에 대응하기 위한 제어 출력이 오프셋 사인 함수에 따라 변조되고 제어값도 이에 따라 조정됩니다.

여기에 타워의 수직 동적 응답을 감소시키기 위한 선형 피드백 제어는 액추에이터에 대한 힘 명령이 프로그램의 7가지 동적 측정의 지정된 가중 선형 합계가 됩니다. 7가지 측정은 다음과 같습니다: TMD 및 상부의 가속도, TMD 및 타워의 속도, TMD 및 타워의 변위, 그리고 타워의 상대적 변위에 대한 TMD. 중요한 점은 가중 계수가 단순하며 양이나 음의 스칼라 값이라는 것입니다. 가중 계수의 매개변수 설정은 타워의 실험적 동적 테스트를 기반으로 합니다. 액추에이터 피드백은 작동 중이며 즉시 계산됩니다(50Hz)
그리고 가중 계수는 스칼라 값이며, 이러한 계수는 어떠한 형태의 진동수 종속 전달 함수도 사용하지 않습니다. 따라서 이 피드백은 동적 속성의 선형 결합입니다. 사용되고 있는 비선형 조작 또는 로직은 없습니다. 제어 설계이 시간 영역에서의 수치 시뮬레이션(직접 통합)을 위해 이루어졌으므로, 각 시간 단계에 대해 액추에이터 제어로서 TMD 질량에 대한 강제 입력을 조절할 수 있었습니다. 그림 12는 진동 억제에 대한 시뮬레이션에서 나온 결과를 보여줍니다. 즉, 타워 변위 및 이로 인한 TMD 질량의 이동 거리입니다.


여기 모드의 경우, 타워가 원하는 변위 값으로 여기되는 것을 나타내는 오프셋과 함께 동일한 제어 접근 방식이 사용되었습니다. 이 오프셋은 각 방향에 대해 감지된 기본 진동수를 기반으로 한 사인 함수입니다. 그러면 방해 요소에 의한 상부 변위의 진동에 대응하기 위한 제어 출력이 오프셋 사인 함수에 따라
변조되고 제어값도 이에 따라 조정됩니다. 이 오프셋에 대해 가중 계수가 실험에 의해 결정되었습니다. 그림 13은 단순 사인 곡선 여기와 제어 알고리즘이 적용된 여기 모드에 대한 돌풍 하중 방해에 대한 결과를 수치적으로 제시합니다.


8.0 안전 컨셉
액추에이터로 사용된 선형 드라이브가 제공할 수 있는 +/- 40kN의 힘을 고려하면, 타워 변위가 피로 규정을 초과하지 않는 것을 보장하는 안전 개념이 필수적입니다. 이는 힘의 출력이 충분하지 않아 상부 편향이 사전에 규정된 +/-200mm보다 크지 않는 경우에도 적용됩니다. 시스템의 안전을 더욱 개선하는 한 가지 방법은 타워의 상단 편향을 기록하는 모니터링 센서 중복을 증가시키는 것입니다. 이를 달성하기 위한 가장 좋은 방법은 실제 제어 하드웨어와 다른 측정 원리를 이상적으로 사용하는 독립된 모니터링 시스템을 추가하는 것입니다. 여기서 소개한 프로젝트의 경우, 사용한 제어 하드웨어는 이미 언급한 것과 같이 가속도계와 구조물의 관련 고유 진동수 범위 내에서 신호 대역 필터링을 위한 정의된 가속 임계값을 사용하였습니다. 가장 중요한 상위 모니터링 시스템은 정확도가 +/- 10mm인 세계 항행 위성 시스템(Global Navigation Satellite System: GNSS)입니다. 이 GNNS 시스템에는 좌표 데이터를 실제 변위 응답값으로 처리하는 기준 베이스 스테이션이 필요합니다. 타워의 상부 변위가 인위적인, 즉 추가적인 바람이나 기타 다른 여기에 의한 것일 수 있는 여기 모드 중 사전에 지정된 임계값을 초과하면, 릴레이가 출석 신호를 0V로 전환합니다. 그러면 여기 모드가 중단될 것입니다. 또한 두 모니터링 시스템은 수집한 데이터에 결함이 있는 센서 신호가 있는지 여부를 지속적으로 점검하여, 활성 여기 모드가 중단됩니다. 잘못된 가속/스트링 포트 신호는 스펙트럼 극대값 검출 기준에 의해 감지됩니다. 관련 범위 내에서의 극대값 검출이 가능한 경우에만 센서가 올바른 신호를 제공한다고 가정할 수 있습니다. GNNS 시스템이 좌표 데이터의 변경을 분석할 때, 샘플링한 데이터가 적시에 변경되지 않으면, 그 신호는 자동으로 틀린 신호로 간주됩니다.
9.0 진동 테스트
타워에 대한 최초의 진동 테스트는 그 타워가 아직 준공되지 않은 단계에서 수행되었기 때문에, 이 단계에서 타워의 기본 진동수는 피동형 TMD 시스템의 명시된 동조 범위 이상입니다. TMD를 가능한 한 가장 높은 동조 진동수로 조절하였습니다. 이 진동 테스트의 목표는 차단된 TMD 시스템과 고유한 구조적 댐핑력을 사용하여 타워의 기본 진동수를 측정하는 것이었습니다. 또한 피동형 TMS 시스템을 연결했을 때의 진동 거동과 피동형 TMD 시스템으로 인한 구조적 댐핑력의 증가도 측정할 것입니다. 타워의 기본 고유 진동수를 확인하기 위해 평균 정규화 파워 스펙트럼 밀도(Averaged Normalized Power Spectral Density: ANPSD) 방식을 [1] 사용할 수 있습니다. 이를 위해 기록한 시간 이력을 여러 세그먼트로 분리했습니다. 이러한 세그먼트를 진동수 영역으로 변환시켜야 합니다. 결과로 얻은 스펙트럼을 정규화 및 평균화하여 복소 공액 스펙트럼으로 곱해야 합니다.
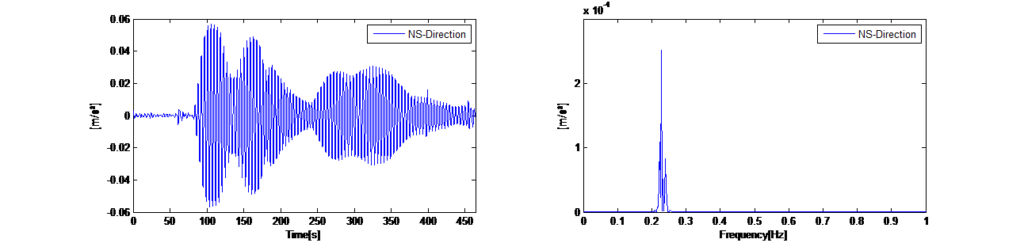
이렇게 하면, 일정하기 않은 진동이 모두 제거되고 반복적으로 발생하는 구조물의 자유 진동만이 평균 스펙트럼에 표시되며, 이것은 이제 타워의 여기된 우세 고유 진동수를 나타냅니다. 그림 14는 차단된 TMD 사용 시, x 및 y 방향에서의 수평 주변 진동에 대해 기록한 시간 이력을 나타냅니다 그림 14 우측에는 120초의 세그먼트 길이에 대한 평균 오토 파워 스펙트라(Auto Power Spectra)가 표시되어 있습니다. 이 스펙트럼은 타워가 두 진동수(x 방향에서 0.225Hz 및 y 방향에서 0.245Hz)에서 동적 응답을 보인다는 것을 확인할 수 있도록 합니다.
주변 여기가 관련 진동 모드에서 충분한 동적 응답을 유발하여 확률적으로 안정성을 얻는다고 가정하는 위에서 설명한 평균 전력 스펙트럼 방법에 추가적으로, 고유 주파수는 상용 신호 처리 소프트웨어인 ARTEMIS를 사용하여 결정되었습니다. [1] 이 소프트웨어는 개선된 주파수 영역 분해(Enhanced Frequency Domain Decomposition) 및 확률적 부분공간 식별(Stochastic Subspace Identification) 방법을 통합합니다.

개선된 주파수 영역 분해(Enhanced Frequency Domain Decomposition: EFDD)와 확률적 부분공간 식별(Stochastic Subspace Identification)은 출력 전용 모달 매개변수 식별에 널리 사용되는 기법입니다.


EFDD 방식은 응답 스펙트럼의 계산을 기반으로 합니다. 그러므로 스펙트럼 평가에서 오류를 낮추고 모달 매개변수를 신뢰할 수 있는 방법으로 추출하기 위해서는 장기간의 기록이 필요합니다. 출력 전용 모델을 사용하여 교량을 확인하기 위해 확률적 부분공간 식별 알고리즘을 적용하였습니다. 확률적 부분공간 식별 방식은 시간 영역에서 사용되며 동적 문제의 상태 공간 설명을 기반으로 합니다. 서로 다른 모델 차수의 시스템 식별 결과를 비교하여, 소위 안정화 도표라고 하는 것에서 실제 구조 모드를 스퓨리어스 모드와 구별하였습니다. 이 도표는 확인된 시스템 모델을 선택할 때 일반적으로 사용되는 방법입니다. 실제 구조 모드는 자동화된 절차에서 평가된 특정 안정화 기준을 충족시키며 연속적인 모델 순서에 대해 안정적인 경향을 보이기 때문입니다. 그림 15는 관련 모드를 결정할 수 있도록 기록된 주변 데이터에 대한 결과 안정성 카드를 보여줍니다. 확인된 모드와 차단된 TMD(좌측) 및 연결된 TMD(우측)를 사용한 상태에서 측정한 감쇠율은 그림 14에도 표시되어 있습니다. 구조적 감쇠 증가를 확인할 수 있습니다. 추가적인 구조적 감쇠는 비동조 TMD 설정을 고려한 이론적 모델에서 결정할 수 있는 이론적 값 범위 내에 있습니다.
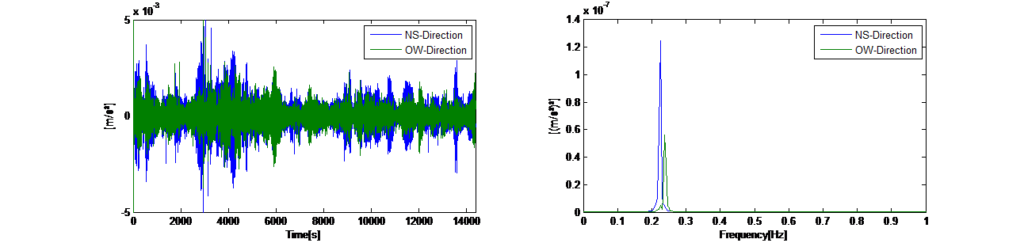
피동형 TMD 시스템을 사용한 주변 진동 테스트 외에도, TMD 시스템이 비동조 상태에 있음에도 불구하고 능동적인 여기 모드를 이용한 예비 테스트를 수행하였습니다. 그림 12 좌측은 타워의 상부에서 기록한 가속도에 대한 시간 이력을 나타냅니다. 최초의 사인파 여기 후, 타워 편향과 TMD 질량의 강제 변위 사이의 상관 관계를 실험적으로 측정하기 위해 정상 상태의 가속도 레벨을 위한 알고리즘을 이용할 수 있었습니다. 그림 12에 표시된 시간 이력은 여기 모드에서의 두 가지 테스트 시나리오를 나타내고 이에 상응하는 FFT 스펙트럼은 타워가 두 기본 주파수(x 및 y 방향)로 보내는 명확한 응답을 표시합니다. 녹색으로 표시된 시간 영역은 두 기본 방향에서 동적 응답을 야기한, 능동형 제어가 비활성화된 질량의 사인파 여기입니다. 이로 인한 FFT 스펙트럼은 이 두 방향의 기본 진동수를 식별하기 위한 두 극대값을 나타냅니다. 청색으로 표시된 세그먼트는 활성화된 능동형 제어가 있는 여기를 위한 것으로, 이는 한 방향에서 우세한 더 안정적인 타워 변위를 유발합니다. 여기 모드가 꺼진 후 발생하는 진동 약화는 구조적 댐핑을 측정하기 위해 사용되었으며, D=2.4%로 결정되었습니다. 이 결과는 SSI 알고리즘으로 결정한 감쇠율과 상관 관계가 있습니다.

10.0 결론 및 전망
Dual Use TMD를 246m 높이의 Thyssen Krupp Test-Tower에 설치했으며, 그 목표는 이 타워를 자체적인 기본 진동수로에서 제어된 동적 응답으로 의도적으로 여기시키는 것이었습니다. 이러한 여기의 목표는 타워의 두 기본 방향에서 건물을 정의된 바와 같이 흔드는 것입니다. 수치 계산을 기반으로 하여, 피동 모드에서 필요한 추가적인 감쇠를 달성하고 +/- 200mm의 타워 상부 변위를 달성하기 위해 필요한 제어력을 생성하기 위해서는 240톤의 TMD 질량이 필요하다는 것이 밝혀졌습니다. 여기 모드에 대해 정상 상태의 변위 레벨를 생성하고 직각 방향에서 바람과 강제 진동 요소에 의해 야기된 변위를 억제하기 위해 제어 알고리즘을 개발하고 수치 시뮬레이션으로 이를 테스트하였습니다. 사전에 제작된 콘크리트 슬래브를 사용한 진자 유형의 피동형 TMD 시스템을 설치한 후 액추에이터를 시운전하여 최초의 테스트를 수행하였습니다. 이 테스트로 타워의 고유 감쇠력이 예상했던 것보다는 높다는 것을 확인했으나 관련된 모든 모드를 명확히 결정할 수 있었습니다. 건물의 능동형 여기 모드가 작동하고 있으며, 건물이 아직 완전히 완성되지 않았기 때문에 모든 작동 매개변수를 도출할 수 있는 전체 범위는 아니지만 테스트를 실행할 수 있었습니다. 건물이 아직 완성 단계에 있지 않았기 때문에 TMD를 측정된 기본 진동수에 맞추어 조절할 수 없었습니다.
TMD 시스템을 조절하는 즉시, 진폭에 따른 댐핑 및 안전 개념의 무결성에 관한 테스트를 포함하여, 빌딩에 대한 후속 테스트가 수행됩니다.
참고 자료
[1] Wenzel, H., Pichler, D., Schedler, R. (1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.: Mevel, L. (2012). “Operational Modal Analysis using a Fast Stochastic Subspace Identification Method”, Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T., Spencer, J.R. (2000). “Active, Semi-Active and hybrid control of structures” In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Passive and active mass damper control of the response of tall buildings to wind gustiness. Eng. Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24–29.
[8] Soong, T.T. “Active Structural Control: Theory and Practice”; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008).”Active Control of Structures”, Wiley, Padstow
1.0 들어가는 말/ 이력
독일 남서부에 높이 246m의 엘레베이터 기술개발을 위한 고층의 대형 테스트 타워는 원형의 직경 20m 면적에 준공되었으며, 내부에 엘레베이터 통로 9개, 방재승강기 1대, 통유리 파노라마 뷰 엘레베이터 공간과 함께 엘레베이터 성능검사를 위한 220m의 기계 리프팅 통로가 마련되어 있습니다.
직경 40m의 빌딩 기초부에는 별도의 서비스 시설 및 로비, 교육 센터 공간이 있습니다. 232m 높이에 위치한 관측대는 독일에서 가장 높은 관측대로 슈바르츠발트의 멋진 경관을 확인할 수 있으며, 맑은 날씨에는 알프스 산맥까지 볼 수 있습니다.

2.0 구조 시스템:
테스트타워 빌딩의 구조시스템은 직경 20.8m의 철근 콘크리트 튜브를 기본으로 구성되어 있으며 지하 30m 깊이로 건물 둘레의 지반에 고정됩니다 (그림 2 참조). 해당 튜브는 높이 110m 까지는 두께가 40cm이고 그 위로는 25cm입니다. 기반이 상부 육성층과 하부 해성층으로 구성된 경우, 지지력이 높아 별도의 파일 기초가 필요하지 않습니다. 건축물이 넓은 지반에 고정되어 있는 동시에, 기초구조물의 규모가 넓어 수평강성이 더욱 높아졌습니다.
콘크리트 튜브의 내구성은 주로 승강기 통로의 내벽에 의해 결정됩니다. 엘리베이터에 접근할 수 있도록 특정 층에만 조립식 천장슬래브가 설치되어 있습니다. 일부 엘리베이터는 115m 높이로 현장에서 주조된 40cm 두께의 대경간으로 덮여 있습니다. 해당 층은 오피스 공간으로 사용되고 있습니다. 위로 197m 정도의 빈 공간에 열 저장체와 TMD 제진시스템가 설치되었습니다. 타워의 정상은 사무실 및 기타 엘리베이터를 위한 공간으로 사용되었습니다.

이 테스트 타워만의 독특한 특징은 PTFE 코팅의 유리섬유메시로 직물 외벽을 구성했다는 점입니다. 건물이 높아질수록 섬유메시를 더 넓은 폭으로 설치하여, 외벽의 투명도를 높이는 동시에 소재의 밀도와 중량을 낮추고 풍하중에 대한 저항도를 향상시켰습니다.
나선형의 외벽 디자인은 ‘Scructon Spiral’ 로 불리는 형태로, 풍하중 방지하는 동시에, 섬유망으로 콘크리트 구조물에 그늘을 만들어 태양 복사열까지 감소시키는 기능을 가지고 있습니다. 이 경우 외벽 설계와 건축재를 선택할 때에 시공과 유지관리, 내구성 외에 풍하중까지 함께 고려되어야 했습니다.
3.0 건축 공법

테스트 타워의 시공절차:
- 30m 원형수직구 지반 굴착 발파공법으로 굴착 및 모델링을 실시했습니다. 굴착 후 지반앵커와 콘크리트 보강벽체로 기초를 완성했습니다.
- 매트기초 타설
- 슬립 폼 공법으로 수직구 시공 4개월간 수직구 벽체 완공
- 기초슬래브 시공
- 출입구역 시공
4.0 풍하중에 대한 동적응답 예측
테스트 타워의 기본 진동수는 건축 단계와 콘크리트의 상태(균열/비균열)에 따라 0.17Hz – 0.20Hz의 범위 내에 있을 것으로 예측하였습니다 – 그림 4 참조.

풍동 해석을 통해 55 – 60km/h 범위 내의 풍속에서 높이 10m에 해당하는 구조물 공진이 발생할 수 있다고 예측되었습니다. 추가적인 제진장치 없이는 진동이 약 +/- 750mm의 상층부 처짐을 유발하여, 건물 이용자들에게 불안감을 줄 뿐만 아니라, 전체 건축물 자체 수명에 상당한 영향을 줄 수 있다는 결론이 나왔습니다. (그림 5 참조). 횡방향 풍진동에 대한 동적응답을 줄이기 위해 수동형 TMD 제진시스템이 도입되었습니다. 타워가 건물의 흔들림에 민감한 승강기 설비에 대한 테스트 타워로 사용될 것이기 때문에, 발주자는 바람이 없는 날 인위적으로 타워를 흔들어, 그럼에도 불구하고 어떠한 피로 문제가 발생하지 않는 변위를 발생시킬 수 있는 방법을 찾았습니다. 인위적인 흔들림에 필요한 수준은 약 +/- 200mm라고 간주한 안전 범위 이내였습니다. 이러한 요청으로 인해 하이브리드 질량 댐퍼(Hybrid Mass Damper: HMD), 또는 이렇게 설계한 시스템이 과거에 도입된 다른 HMD 시스템에서 파생되었기 때문에 Dual Use TMD라고 칭하는 시스템을 구현할 수 있는 드문 기회가 주어졌습니다. 이 시스템은 다음 장에서 소개할 계정이며, 여기에는 피동형 시스템의 최적화, 액추에이터의 기계 장치 설계, 제어 알고리즘 및 안전 컨셉이 포함되어 있습니다.

5.0 피동형 TMD 제진 시스템의 최적화
피동형 TMD 시스템의 매개변수는 다음과 같은 세 가지 측면을 고려하여 결정되어야 합니다: a) 와류 발산 진동으로 인한 동적 응답을 감소시키기 위한 추가적인 구조적 댐핑력을 충분히 제공, b) 돌풍 발생 시 횡방향 풍진동에 대해, 피동 모드에서 충분한 댐핑력으로 TMD 메인 질량 이동을 달성할 수 있는/실제 값으로 제한, c) 공급한 액추에이터에 의해 이용할 수 있는 성능 범위를 고려하여, 타워의 원하는 최대 편향에 필요한 에너지 유입에 따라 여기 모드에서 TMD 질량 선택(예: 발생한 최대 힘 및 작동 중 최대 스트로크). TMD 시스템을 최적화하기 위해 확인된 구조적 속성에서 보고된 것과 동일한 질량 관성 모멘트와 타워의 질량 분배를 나타내는 수치 모델을 사용하였습니다. 실물 크기의 관찰에서 나온 모드 형상과 고유 진동수를 일치시키기 위해 바닥판 사이의 강성 부재를 맞춤형으로 제조하였습니다. 그림 6 좌측에는 사용한 해당 아날로그 모델의 모드 형상과 고유 진동수가 표시되어 있습니다. 또한 그림 6 좌측에서는 아날로그 모델의 모드 형상을 구조 컨설턴트가 준비한 상세한 모델의 모드 형상과 비교하고 있습니다.


또한 TMD는 타워에서 자신의 편향된 위치를 수집하며, 진자형 시스템으로 별도로 모델화되었습니다. 통제적 입력 케이스를 위한 하중 특성은, 예를 들어 와류 발산으로 인한 공진 여기는 단일 조화 여기의 특성과 상당히 유사합니다. 그럼에도 불구하고 공존하는 돌풍 하중은 그 특성이 본질적으로 확률적이라는 점이며, 이를 위해 잘 알려진 Den Hartog 기준과 다른 최적화 기준이 적용됩니다. 또한 TMD 질량의 상대적 변위는 조화 유형의 하중보다 확률적 유형에서 더 큽니다. 최적의 TMD 매개변수를 수치로 결정하기 위해서는 실제에 가까운 하중을 고려해야 하기 때문에, (다벤포트 스펙트럼 기반) 확률적 돌풍 하중과 겹친 공진을 와류 발산과 유사한, 즉, 전반적인 횡방향 풍진동을 나타내기 위한 요소를 포함한 시간 이력을 생성하였습니다(그림 3 우측 참조). 최적화된 피동형 TMD 시스템으로 달성할 수 있는 타워의 편향 감소와 그로 인한 TMD 변위는 그림 3 우측에 표시되어 있습니다. ξ=0.8%로 산정한 고유의 구조적 댐핑에 대한 이러한 결과를 기초로 하여, 최고의 TMD 성능을 위해 최적의 TMD 감쇠율을 유지하면서 +/- 650mm의 변위를 유지하려면 240톤의 TMD 질량이 필요했다고 판단했습니다. TMD 댐핑의 증가는 이동 거리를 감소시킬 수 있었습니다. 그 효율성은 여전히 충분하지만 이는 역으로 액추에이터의 힘에 대한 요구 사항에 영향을 주었습니다. 240톤 TMS를 최적으로 설치하기 위해 필요한 힘을 결정하기 위해, 아날로그 모델도 사용하여 타워의 변위가 +/- 200mm의 범위 내에서 이루어질 수 있다는 점을 검증하였으며, 이때 액추에이터에서 나온 최대 40kN의 힘을 사용하였습니다. 그림 4에는 아날로그 수치 모델을 사용한 시간 영역 수치 시뮬레이션 결과가 표시되어 있습니다; 이를 위해 결과적으로 발생한 타워 상부의 편향, TMD 질량 편향 및 이를 유발하는 유입된 능동적인 힘이 표시되어 있습니다.


6.0 제어 시스템에 대한 설명
제어 시스템의 이중성은 다음의 목적을 달성합니다: a) 정상적인 피동형 작동 중 진동 발생을 줄이기 위한 에너지 소비 감소 b) 실제로 요구되는 힘을 궁극적으로 달성하기 위해, 메인 TMD 질량 자극을 위한 공진 효과를 사용함으로써 액추에이터에 요구하는 힘의 감소 따라서 다른 제어 시스템(그림 1 참조)과 비교하자면, 액추에이터는 메인 구조물과 TMD 질량을 결합하지만 TMD 질량을 직접 제어하기 위해서는 사용되지 않습니다. 이러한 제어는 전형적인 능동형 질량 드라이버/댐퍼 시스템이 담당하기 때문입니다. 구현된 Dual Use TMD를 위해 240톤의 피동형 작동을 위한 반응 질량이 선택되었습니다. 여자 작동 모드의 경우 두 개의 선형 드라이브(각 주요 방향에 하나씩)의 인위적인 비틀림을 방지하기 위해 무게 중심 근처에 피벗이 있는 TMD 질량에 부착됩니다. 각 선형 드라이브는 최대 +/- 600mm의 스트로크 내에서 최고 40kN의 힘을 공급할 수 있습니다(세부 사항에 대해서는 그림 2 참조). 선형 드라이브는 탈거할 수 있으므로, 발생 가능성이 극히 낮으나 베어링 고장 시에도 액추에이터의 베어링에 의해 피동 모드 전체가 영향을 받지는 않습니다.


이 시스템에는 타워 상부의 높이 및 TMD 질량 가속도를 측정하기 위해 네 개의 단축 가속도계(지진 K-빔/MEMS; 각 방향에 하나씩)가 장착되어 있습니다. 가속 신호는 타워가 가지고 있는 기본적인 고유 주파수(0.1 – 0.3Hz)의 주파수 범위 내에서 대역 필터링되고, 타워의 가속도와 편향에 통합됩니다. 또한 신호 드리프트를 비교하기 위해 상부에도 설치한 무료 세계 항행 위성 시스템(Global Navigation Satellite System) 중 하나와 통합된 변위 값을 비교할 수 있습니다. 최초의 관련 테스트를 적절하게 수행했습니다. 더 나아가 스트링 포트 변환기를 사용하여 TMD 변위를 직접 모니터링하였으며 유도형 길이 측정 시스템을 선형 모터 내에 내장하였습니다.
7.0 제어 알고리즘
타워에 대한 일반적인 제어 루프는 폐쇄루프 제어 시퀀스를 설명한 그림 5에 표시되어 있습니다. 제어 알고리즘을 세부적으로 설계하기 위해서는 액추에이터-TMS 질량 사이의 상호 작용에 대한 분석적 모델이 필요합니다. 이는 적용된 작용력에 대해 액추에이터 입력부 사이의 연결을 결정하기 위해서입니다. 이것은 전체 건물의 동적 거동을 설명하는 주요 구조 해석 모델과 결합되어야 합니다. 더 나아가, 다음과 같이 다른 HMD 애플리케이션에 적용되었던 표준 제어 알고리즘과 비교 [2],[3] 또는 다음과 같이 이론적으로 조사 [1] 이 타워 애플리케이션에 대한 제어 알고리즘은 하나의 메인 방향에서의 제어된 여기와 직각 방향에서의 진동 감소를 동시에 고려해야 했습니다. 기본 모드에서는 대부분 동적 응답을 예상하므로, 불안전성을 방지하는 데 장점이 있는 선형 피드백 제어를 이 두 작업에 적용할 수 있었습니다. 단순한 제어를 실제로 구현하기 위해, 타워의 여기에 대한 수직 동적 반응을 약화시시키는 선형 피드백 제어는 7가지 동적 측정에 대한 명시적으로 가중된 선형 합계를 통해 관련 액추에이터를 작동시킵니다. 이 측정은 다음과 같습니다: TMD 및 타워 상부의 가속도, TMD 및 타워 상부의 속도, TMD 및 타워 상부의 변위, 그리고 타워 상부의 상대적 변위에 대한 TMD. 중요한 점은 사전에 선택한 가중 계수가 단순하며 양이나 음의 스칼라 게인라는 것입니다. 가중 계수의 매개변수 설정은 타워의 동적 테스트를 기반으로 하며 진동수에 종속된 어떠한 변경도 사용하지 않습니다. 능동적인 액추에이터 피드백을 즉시 (50Hz에서) 계산하며, 이는 다시 기존의 동적 측정의 선형 결합이 됩니다. 사용되는 비선형 조작은 없습니다. 제어 설계 역시 액추에이터 제어에 의해 진동 감쇠가 이루어진다는 것을 증명하는 시간 영역 수치 시뮬레이션(예: 직접 통합)으로 이루어졌습니다. 여기 모드의 경우, 타워가 원하는 변위 값으로 여기되는 것을 나타내는 변위 오프셋과 함께 동일한 제어 접근 방식이 사용되었습니다. 이 오프셋은 각 방향의 감지된 기본 진동수를 기반으로 한 사인 함수입니다. 그러면 다른 방해 요소에 의한 상부 변위의 진동에 대응하기 위한 제어 출력이 오프셋 사인 함수에 따라 변조되고 제어값도 이에 따라 조정됩니다.

여기에 타워의 수직 동적 응답을 감소시키기 위한 선형 피드백 제어는 액추에이터에 대한 힘 명령이 프로그램의 7가지 동적 측정의 지정된 가중 선형 합계가 됩니다. 7가지 측정은 다음과 같습니다: TMD 및 상부의 가속도, TMD 및 타워의 속도, TMD 및 타워의 변위, 그리고 타워의 상대적 변위에 대한 TMD. 중요한 점은 가중 계수가 단순하며 양이나 음의 스칼라 값이라는 것입니다. 가중 계수의 매개변수 설정은 타워의 실험적 동적 테스트를 기반으로 합니다. 액추에이터 피드백은 작동 중이며 즉시 계산됩니다(50Hz) 그리고 가중 계수는 스칼라 값이며, 이러한 계수는 어떠한 형태의 진동수 종속 전달 함수도 사용하지 않습니다. 따라서 이 피드백은 동적 속성의 선형 결합입니다. 사용되고 있는 비선형 조작 또는 로직은 없습니다. 제어 설계이 시간 영역에서의 수치 시뮬레이션(직접 통합)을 위해 이루어졌으므로, 각 시간 단계에 대해 액추에이터 제어로서 TMD 질량에 대한 강제 입력을 조절할 수 있었습니다. 그림 12는 진동 억제에 대한 시뮬레이션에서 나온 결과를 보여줍니다. 즉, 타워 변위 및 이로 인한 TMD 질량의 이동 거리입니다.


여기 모드의 경우, 타워가 원하는 변위 값으로 여기되는 것을 나타내는 오프셋과 함께 동일한 제어 접근 방식이 사용되었습니다. 이 오프셋은 각 방향에 대해 감지된 기본 진동수를 기반으로 한 사인 함수입니다. 그러면 방해 요소에 의한 상부 변위의 진동에 대응하기 위한 제어 출력이 오프셋 사인 함수에 따라 변조되고 제어값도 이에 따라 조정됩니다. 이 오프셋에 대해 가중 계수가 실험에 의해 결정되었습니다. 그림 13은 단순 사인 곡선 여기와 제어 알고리즘이 적용된 여기 모드에 대한 돌풍 하중 방해에 대한 결과를 수치적으로 제시합니다.


8.0 안전 컨셉
액추에이터로 사용된 선형 드라이브가 제공할 수 있는 +/- 40kN의 힘을 고려하면, 타워 변위가 피로 규정을 초과하지 않는 것을 보장하는 안전 개념이 필수적입니다. 이는 힘의 출력이 충분하지 않아 상부 편향이 사전에 규정된 +/-200mm보다 크지 않는 경우에도 적용됩니다. 시스템의 안전을 더욱 개선하는 한 가지 방법은 타워의 상단 편향을 기록하는 모니터링 센서 중복을 증가시키는 것입니다. 이를 달성하기 위한 가장 좋은 방법은 실제 제어 하드웨어와 다른 측정 원리를 이상적으로 사용하는 독립된 모니터링 시스템을 추가하는 것입니다. 여기서 소개한 프로젝트의 경우, 사용한 제어 하드웨어는 이미 언급한 것과 같이 가속도계와 구조물의 관련 고유 진동수 범위 내에서 신호 대역 필터링을 위한 정의된 가속 임계값을 사용하였습니다. 가장 중요한 상위 모니터링 시스템은 정확도가 +/- 10mm인 세계 항행 위성 시스템(Global Navigation Satellite System: GNSS)입니다. 이 GNNS 시스템에는 좌표 데이터를 실제 변위 응답값으로 처리하는 기준 베이스 스테이션이 필요합니다. 타워의 상부 변위가 인위적인, 즉 추가적인 바람이나 기타 다른 여기에 의한 것일 수 있는 여기 모드 중 사전에 지정된 임계값을 초과하면, 릴레이가 출석 신호를 0V로 전환합니다. 그러면 여기 모드가 중단될 것입니다. 또한 두 모니터링 시스템은 수집한 데이터에 결함이 있는 센서 신호가 있는지 여부를 지속적으로 점검하여, 활성 여기 모드가 중단됩니다. 잘못된 가속/스트링 포트 신호는 스펙트럼 극대값 검출 기준에 의해 감지됩니다. 관련 범위 내에서의 극대값 검출이 가능한 경우에만 센서가 올바른 신호를 제공한다고 가정할 수 있습니다. GNNS 시스템이 좌표 데이터의 변경을 분석할 때, 샘플링한 데이터가 적시에 변경되지 않으면, 그 신호는 자동으로 틀린 신호로 간주됩니다.
9.0 진동 테스트
타워에 대한 최초의 진동 테스트는 그 타워가 아직 준공되지 않은 단계에서 수행되었기 때문에, 이 단계에서 타워의 기본 진동수는 피동형 TMD 시스템의 명시된 동조 범위 이상입니다. TMD를 가능한 한 가장 높은 동조 진동수로 조절하였습니다. 이 진동 테스트의 목표는 차단된 TMD 시스템과 고유한 구조적 댐핑력을 사용하여 타워의 기본 진동수를 측정하는 것이었습니다. 또한 피동형 TMS 시스템을 연결했을 때의 진동 거동과 피동형 TMD 시스템으로 인한 구조적 댐핑력의 증가도 측정할 것입니다. 타워의 기본 고유 진동수를 확인하기 위해 평균 정규화 파워 스펙트럼 밀도(Averaged Normalized Power Spectral Density: ANPSD) 방식을 [1] 사용할 수 있습니다. 이를 위해 기록한 시간 이력을 여러 세그먼트로 분리했습니다. 이러한 세그먼트를 진동수 영역으로 변환시켜야 합니다. 결과로 얻은 스펙트럼을 정규화 및 평균화하여 복소 공액 스펙트럼으로 곱해야 합니다.
이렇게 하면, 일정하기 않은 진동이 모두 제거되고 반복적으로 발생하는 구조물의 자유 진동만이 평균 스펙트럼에 표시되며, 이것은 이제 타워의 여기된 우세 고유 진동수를 나타냅니다. 그림 14는 차단된 TMD 사용 시, x 및 y 방향에서의 수평 주변 진동에 대해 기록한 시간 이력을 나타냅니다 그림 14 우측에는 120초의 세그먼트 길이에 대한 평균 오토 파워 스펙트라(Auto Power Spectra)가 표시되어 있습니다. 이 스펙트럼은 타워가 두 진동수(x 방향에서 0.225Hz 및 y 방향에서 0.245Hz)에서 동적 응답을 보인다는 것을 확인할 수 있도록 합니다.
주변 여기가 관련 진동 모드에서 충분한 동적 응답을 유발하여 확률적으로 안정성을 얻는다고 가정하는 위에서 설명한 평균 전력 스펙트럼 방법에 추가적으로, 고유 주파수는 상용 신호 처리 소프트웨어인 ARTEMIS를 사용하여 결정되었습니다. [1] 이 소프트웨어는 개선된 주파수 영역 분해(Enhanced Frequency Domain Decomposition) 및 확률적 부분공간 식별(Stochastic Subspace Identification) 방법을 통합합니다.

개선된 주파수 영역 분해(Enhanced Frequency Domain Decomposition: EFDD)와 확률적 부분공간 식별(Stochastic Subspace Identification)은 출력 전용 모달 매개변수 식별에 널리 사용되는 기법입니다.


EFDD 방식은 응답 스펙트럼의 계산을 기반으로 합니다. 그러므로 스펙트럼 평가에서 오류를 낮추고 모달 매개변수를 신뢰할 수 있는 방법으로 추출하기 위해서는 장기간의 기록이 필요합니다. 출력 전용 모델을 사용하여 교량을 확인하기 위해 확률적 부분공간 식별 알고리즘을 적용하였습니다. 확률적 부분공간 식별 방식은 시간 영역에서 사용되며 동적 문제의 상태 공간 설명을 기반으로 합니다. 서로 다른 모델 차수의 시스템 식별 결과를 비교하여, 소위 안정화 도표라고 하는 것에서 실제 구조 모드를 스퓨리어스 모드와 구별하였습니다. 이 도표는 확인된 시스템 모델을 선택할 때 일반적으로 사용되는 방법입니다. 실제 구조 모드는 자동화된 절차에서 평가된 특정 안정화 기준을 충족시키며 연속적인 모델 순서에 대해 안정적인 경향을 보이기 때문입니다. 그림 15는 관련 모드를 결정할 수 있도록 기록된 주변 데이터에 대한 결과 안정성 카드를 보여줍니다. 확인된 모드와 차단된 TMD(좌측) 및 연결된 TMD(우측)를 사용한 상태에서 측정한 감쇠율은 그림 14에도 표시되어 있습니다. 구조적 감쇠 증가를 확인할 수 있습니다. 추가적인 구조적 감쇠는 비동조 TMD 설정을 고려한 이론적 모델에서 결정할 수 있는 이론적 값 범위 내에 있습니다. 피동형 TMD 시스템을 사용한 주변 진동 테스트 외에도, TMD 시스템이 비동조 상태에 있음에도 불구하고 능동적인 여기 모드를 이용한 예비 테스트를 수행하였습니다. 그림 12 좌측은 타워의 상부에서 기록한 가속도에 대한 시간 이력을 나타냅니다. 최초의 사인파 여기 후, 타워 편향과 TMD 질량의 강제 변위 사이의 상관 관계를 실험적으로 측정하기 위해 정상 상태의 가속도 레벨을 위한 알고리즘을 이용할 수 있었습니다. 그림 12에 표시된 시간 이력은 여기 모드에서의 두 가지 테스트 시나리오를 나타내고 이에 상응하는 FFT 스펙트럼은 타워가 두 기본 주파수(x 및 y 방향)로 보내는 명확한 응답을 표시합니다. 녹색으로 표시된 시간 영역은 두 기본 방향에서 동적 응답을 야기한, 능동형 제어가 비활성화된 질량의 사인파 여기입니다. 이로 인한 FFT 스펙트럼은 이 두 방향의 기본 진동수를 식별하기 위한 두 극대값을 나타냅니다. 청색으로 표시된 세그먼트는 활성화된 능동형 제어가 있는 여기를 위한 것으로, 이는 한 방향에서 우세한 더 안정적인 타워 변위를 유발합니다. 여기 모드가 꺼진 후 발생하는 진동 약화는 구조적 댐핑을 측정하기 위해 사용되었으며, D=2.4%로 결정되었습니다. 이 결과는 SSI 알고리즘으로 결정한 감쇠율과 상관 관계가 있습니다.

10.0 결론 및 전망
Dual Use TMD를 246m 높이의 Thyssen Krupp Test-Tower에 설치했으며, 그 목표는 이 타워를 자체적인 기본 진동수로에서 제어된 동적 응답으로 의도적으로 여기시키는 것이었습니다. 이러한 여기의 목표는 타워의 두 기본 방향에서 건물을 정의된 바와 같이 흔드는 것입니다. 수치 계산을 기반으로 하여, 피동 모드에서 필요한 추가적인 감쇠를 달성하고 +/- 200mm의 타워 상부 변위를 달성하기 위해 필요한 제어력을 생성하기 위해서는 240톤의 TMD 질량이 필요하다는 것이 밝혀졌습니다. 여기 모드에 대해 정상 상태의 변위 레벨를 생성하고 직각 방향에서 바람과 강제 진동 요소에 의해 야기된 변위를 억제하기 위해 제어 알고리즘을 개발하고 수치 시뮬레이션으로 이를 테스트하였습니다. 사전에 제작된 콘크리트 슬래브를 사용한 진자 유형의 피동형 TMD 시스템을 설치한 후 액추에이터를 시운전하여 최초의 테스트를 수행하였습니다. 이 테스트로 타워의 고유 감쇠력이 예상했던 것보다는 높다는 것을 확인했으나 관련된 모든 모드를 명확히 결정할 수 있었습니다. 건물의 능동형 여기 모드가 작동하고 있으며, 건물이 아직 완전히 완성되지 않았기 때문에 모든 작동 매개변수를 도출할 수 있는 전체 범위는 아니지만 테스트를 실행할 수 있었습니다. 건물이 아직 완성 단계에 있지 않았기 때문에 TMD를 측정된 기본 진동수에 맞추어 조절할 수 없었습니다.
TMD 시스템을 조절하는 즉시, 진폭에 따른 댐핑 및 안전 개념의 무결성에 관한 테스트를 포함하여, 빌딩에 대한 후속 테스트가 수행됩니다.
참고 자료
[1] Wenzel, H., Pichler, D., Schedler, R. (1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.: Mevel, L. (2012). “Operational Modal Analysis using a Fast Stochastic Subspace Identification Method”, Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T., Spencer, J.R. (2000). “Active, Semi-Active and hybrid control of structures” In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Passive and active mass damper control of the response of tall buildings to wind gustiness. Eng. Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24–29.
[8] Soong, T.T. “Active Structural Control: Theory and Practice”; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008).”Active Control of Structures”, Wiley, Padstow
기타 자원
이 주제에 대한 더 자세한 정보가 필요하십니까?
문제가 있으시면 언제든 당사에 연락하시기 바랍니다.
당사의 프로젝트 엔지니어가 곧 답을 드릴 것입니다.
기타 자원
이 주제에 대한 더 자세한 정보가 필요하십니까?
문제가 있으시면 언제든 당사에 연락하시기 바랍니다.
당사의 프로젝트 엔지니어가 곧 답을 드릴 것입니다.